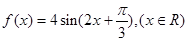Question

关于函数有下列命题：
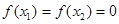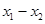①由可得必是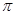的整数倍；②的表达式可改写为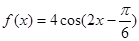；③的图象关于点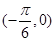对称；④的图象关于直线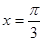对称；⑤在区间上是增函数；其中正确的是（    ）

A．②③⑤

B．①② ③

C．②③ ④

D．①③⑤

Answer 1

A

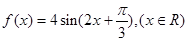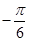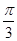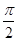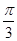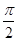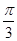试题分析：解：∵ (x∈R)的周期为π，当x₁=-，x₂=时，f（x₁）=f（x₂）=0，x₁-x₂ =≠kπ，k∈z，故①是错误的．∵由诱导公式可得f(x)=4sin(2x+)=4cos（-2x- ）=4cos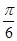（-2x）=4cos（2x-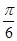），故 ②正确．∵当 x=- 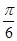时，f（x）=0，故点(-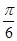，0)是f（x）与x轴的交点，故是对称点，故③正确．∵当 x=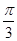时，f(x)=4sin(2x+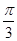)=0，不是f（x）的最值，故④是错误的．由   2kπ-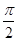≤(2x+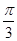)≤2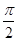kπ+ 得，kπ-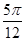≤x≤kπ+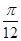，k∈z，故⑤正确．综上，②③⑤正确，①④不正确，答案为 A
点评：本题考查正弦函数的对称性、单调性、周期性，诱导公式的应用，熟记正弦函数的性质是解题的关键．