
【题目】设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
【答案】A
【解析】解:设g(x)= ![]() ,则g(x)的导数为:g′(x)=
,则g(x)的导数为:g′(x)= ![]() ,
,
∵当x>0时总有xf′(x)<f(x)成立,
即当x>0时,g′(x)恒小于0,
∴当x>0时,函数g(x)= ![]() 为减函数,
为减函数,
又∵g(﹣x)= ![]() =
= ![]() =
= ![]() =g(x),
=g(x),
∴函数g(x)为定义域上的偶函数
又∵g(﹣1)= ![]() =0,
=0,
∴函数g(x)的图象性质类似如图:
数形结合可得,不等式f(x)>0xg(x)>0
![]() 或
或 ![]() ,
,
0<x<1或x<﹣1.
故选:A.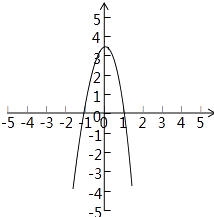
由已知当x>0时总有xf′(x)﹣f(x)<0成立,可判断函数g(x)= ![]() 为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(﹣∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,模拟g(x)的图象,而不等式f(x)>0等价于xg(x)>0,数形结合解不等式组即可.
为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(﹣∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,模拟g(x)的图象,而不等式f(x)>0等价于xg(x)>0,数形结合解不等式组即可.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足 ![]() ,记数列{an}的前n项和为Sn , cn=Sn﹣2n+2ln(n+1)
,记数列{an}的前n项和为Sn , cn=Sn﹣2n+2ln(n+1)
(1)令 ![]() ,证明:对任意正整数n,|sin(bnθ)|≤bn|sinθ|
,证明:对任意正整数n,|sin(bnθ)|≤bn|sinθ|
(2)证明数列{cn}是递减数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=sinxcosx﹣cos2(x+ ![]() ).
).
(1)求f(x)的单调区间;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,若f( ![]() )=0,a=1,求△ABC面积的最大值.
)=0,a=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知条件p:A={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R},条件q:B={x|x2﹣2x﹣3≤0,x∈R}.
(1)若A∩B={x|0≤x≤3},求实数m的值;
(2)若q是¬p的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
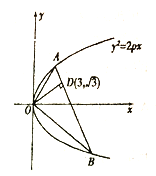
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com