练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆C：.

    （1）求经过点且与圆C相切的直线方程；

    （2）设直线与圆C相交于A，B两点，若，求实数n的值；

    （3）若点在以为圆心，以1为半径的圆上，距离为4的两点P，Q在圆C上，求的最小值.

    【答案】（1）；（2）或；（3）

    【解析】

    （1）点就在圆上，且与圆心横坐标一样，则可直接写出切线方程；

    （2）由数量积的运算可得，则，进而可得圆心到直线的距离，再由点到直线的距离可得实数n的值；

    （3）利用向量的几何运算可得，求出的最小值，即可得最小值.

    解：（1）因为，则点就在圆C上，

    故点就是切点，又圆心为

    则切线斜率为，

    所以经过点且与圆C相切的直线方程；

    （2）∵

    ，又，

    ∴，

    则圆心到直线的距离为，

    ∴或；

    （3）∵

    ，

    ∴当NC最小时，最小，

    ∵，

    ∴当时，取得最小值为，

    此时最小为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知向量， ，设函数，且的图象过点和点.

    （Ⅰ）求的值；

    （Ⅱ）将的图象向左平移（）个单位后得到函数的图象.若的图象上各最高点到点的距离的最小值为1，求的单调增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数在区间上的最大值是最小值是则

    A. 与有关,且与有关 B. 与有关,但与无关

    C. 与无关,且与无关 D. 与无关,但与有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在矩形中, , 为的中点, 为的中点.将沿折起到,使得平面平面（如图）.

    图1 图2

    （Ⅰ）求证: ；

    （Ⅱ）求直线与平面所成角的正弦值；

    （Ⅲ）在线段上是否存在点,使得平面?若存在,求出的值;若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂因排污比较严重，决定着手整治，一个月时污染度为，整治后前四个月的污染度如下表：

    月数

    …

    污染度

    …

    污染度为后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：，，，其中表示月数，、、分别表示污染度．

    （1）问选用哪个函数模拟比较合理，并说明理由；

    （2）若以比较合理的模拟函数预测，整治后有多少个月的污染度不超过．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

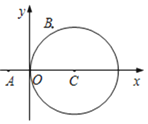
    【题目】如图，在平面直角坐标系xOy中，已知圆C：x2+y2-4x=0及点A（-1，0），B（1，2）

    （1）若直线l平行于AB，与圆C相交于M，N两点，MN=AB，求直线l的方程；

    （2）若圆C上存在两个点P，使得PA2+PB2=a（a＞4），求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知过点的直线与圆相交于A，B两点.

    （1）若，求直线AB的方程；

    （2）设线段AB的中点为M，求点M的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】判断下列命题的真假：

    （1）是的必要条件；

    （2）是的充要条件；

    （3）两个三角形的两组对应角相等是这两个三角形相似的充要条件；

    （4）三角形的三条边满足勾股定理是这个三角形为直角三角形的充要条件；

    （5）在中，重心和垂心重合是为等边三角形的必要条件；

    （6）如果点到点的距离相等，则点一定在线段的垂直平分线上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形是正方形， 平面， // ， ， ， 为的中点．

    （1）求证： ；

    （2）求证： //平面；

    （3）求二面角的大小．

    查看答案和解析>>

    同步练习册答案