
【题目】已知![]() (
(![]() ,且
,且![]() ,
,![]() )是定义在区间
)是定义在区间![]() 上的奇函数,
上的奇函数,
(1)求![]() 的值和实数
的值和实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)若![]() 且
且![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,证明见解析;(3)
上单调递减,证明见解析;(3)![]() .
.
【解析】
(1)根据奇函数的特性,可得![]() ,再由
,再由![]() ,
,![]() ,可得实数
,可得实数![]() 的值;(2)讨论两种情况,当
的值;(2)讨论两种情况,当![]() 时, 当
时, 当![]() 时,分别结合对数函数的图象和性质,及复合函数同增异减的原则,可得函数
时,分别结合对数函数的图象和性质,及复合函数同增异减的原则,可得函数![]() 在区间
在区间![]() 上的单调性;(3)由
上的单调性;(3)由![]() ,可得函数
,可得函数![]() 在区间
在区间![]() 上的单调递增,结合函数的定义域和奇偶性,解不等式,可得实数
上的单调递增,结合函数的定义域和奇偶性,解不等式,可得实数![]() 的取值范围.
的取值范围.
(1)∵![]() (
(![]() ,且
,且![]() ,
,![]() )是定义在区间
)是定义在区间![]() 上的奇函数,
上的奇函数,
∴![]() ,
,
且![]() ,即
,即![]() ,
,
即![]() ,
,
可得![]() ,
,
故![]() ,
,
又∵![]() ,
,
故![]() ,
,
(2)由(1)得![]() ,
,
令![]() ,则
,则![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() 为减函数,此时函数
为减函数,此时函数![]() 在区间
在区间![]() 上的单调递增;
上的单调递增;
当![]() 时,
时,![]() 为增函数,此时函数
为增函数,此时函数![]() 在区间
在区间![]() 上的单调递减;
上的单调递减;
(3)若![]() ,则
,则![]() ,由(1)得,函数
,由(1)得,函数![]() 在区间
在区间![]() 上的单调递增,
上的单调递增,
若![]() ,
,
则![]() ,
,
则![]() ,
,
则![]() ,
,
解得:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若不等式
时,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若方程
时,若方程![]() 在
在![]() 上总有两个不等的实根, 求
上总有两个不等的实根, 求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )
内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测,![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(注:利润与投资额的单位均为万元)
(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1、F2分别是双曲线 ![]() =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为 ( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为 ( ) 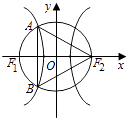
A.![]()
B.2
C.![]() ﹣1
﹣1
D.1+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.
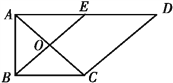
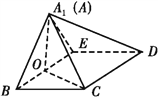
图1 图2
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com