
【题目】在△ABC中,角A.B.C所对的边分别为a.b.c且![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的取值范围是______.
的取值范围是______.
科目:高中数学 来源: 题型:
【题目】下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
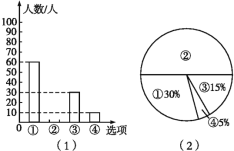
(1)本次一共调查了多少名学生.(2)在图(1)中将②对应的部分补充完整.
(3)若该校有3 000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5时以下?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() ,其中a为常数.
,其中a为常数.
(I)若x=1是函数![]() 的一个极值点,求a的值
的一个极值点,求a的值
(II)若函数![]() 在区间(-1,0)上是增函数,求a的取值范围
在区间(-1,0)上是增函数,求a的取值范围
(III)若函数![]() ,在x=0处取得最大值,求正数a的取值范围
,在x=0处取得最大值,求正数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人单独购买A,B商品分别付款168元和423元,假设他一次性购买A,B两件商品,则应付款是
A. 413.7元 B. 513.7元 C. 546.6元 D. 548.7元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)
分)
已知圆![]() ,过点
,过点![]() 作直线
作直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(Ⅰ)当![]() 经过圆心
经过圆心![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(Ⅱ)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求弦
时,求弦![]() 的长.
的长.
(Ⅲ)求直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)
分)
已知半径为![]() 的圆的圆心在
的圆的圆心在![]() 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线![]() 相切.
相切.
(Ⅰ)求圆的方程.
(Ⅱ)设直线![]() 与圆相交于
与圆相交于![]() ,
, ![]() 两点,求实数
两点,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)在(Ⅱ)的条件下,是否存在实数![]() ,使得点
,使得点![]() 到
到![]() ,
, ![]() 两点的距离相等,若存在,求出实数
两点的距离相等,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() 满足
满足![]() ,
, ![]() ,
, ![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)求和: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据等差数列![]() 的
的![]() ,
, ![]() ,列出关于首项
,列出关于首项![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() 的通项公式;(2)利用已知条件根据题意列出关于首项
的通项公式;(2)利用已知条件根据题意列出关于首项![]() ,公比
,公比![]() 的方程组,解得
的方程组,解得![]() 、
、![]() 的值,求出数列
的值,求出数列![]() 的通项公式,然后利用等比数列求和公式求解即可.
的通项公式,然后利用等比数列求和公式求解即可.
试题解析:(1)设等差数列{an}的公差为d. 因为a2+a4=10,所以2a1+4d=10.解得d=2.
所以an=2n1.
(2)设等比数列的公比为q. 因为b2b4=a5,所以b1qb1q3=9.
解得q2=3.所以![]() .
.
从而![]() .
.
【题型】解答题
【结束】
18
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;命题
;命题![]() :方程
:方程![]() 表示双曲线.
表示双曲线.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com