练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

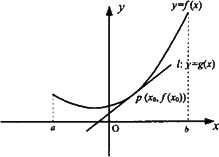
    函数y＝是函数y＝f(x)的导函数，且函数y＝f(x)在点P(x0，f(x0))处的切线为l：y＝g(x)＝(x0)(x－x0)＋f(x0)，F(x)＝f(x)－g(x)，如果函数y＝f(x)在区间[a，b]上的图象如图所示，且a＜x0＜b，那么正确的是

    [　　]
    A．

    (x0)＝0，x＝x0是F(x)的极大值点

    B．

    (x0)＝0，x＝x0是F(x)的极小值点

    C．

    (x0)≠0，x＝x0不是F(x)极值点

    D．

    (x0)≠0，x＝x0是F(x)极值点

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：东台市五烈镇中学2008届高三上学期九月月考(苏教版)、数学理科 题型：013

    已知函数y＝f(x)在(－3，0)上是减函数，又y＝f(x－3)是偶函数，则下列结论正确的是

    [　　]

    A．f(－)＜f(－)＜(－5)

    B．f(－5)＜f(－)＜f(－)

    C．f(－5)＜f(－)＜f(－)

    D．f(－)＜f(－)＜f(－5)

    查看答案和解析>>

    科目：高中数学 来源：贵州省遵义四中2012届高三上学期第四次月考数学文科试题 题型：013

    已知函数y＝f(x)是偶函数，且函数y＝f(x－2)在[0，2]上是单调减函数，则

    [　　]
    A．

    f(－1)＜f(2)＜f(0)

    B．

    f(－1)＜f(0)＜f(2)

    C．

    f(0)＜f(－1)＜f(2)

    D．

    f(2)＜f(－1)＜f(0)

    查看答案和解析>>

    科目：高中数学 来源：辽宁省沈阳二中2008届高三第四次模拟考试(数学) 题型：044

    最小正周期为π的函数(其中a是小于零的常数，是大于零的常数)的图象按向量，(0＜θ＜π)平移后得到函数y＝f(x)的图象，而函数y＝f(x)在实数集上的值域为[－2，2]，且在区间上是单调递减函数．

    (1)求a、和θ的值；

    (2)若角α和β的终边不共线，f(α)＋g(α)＝f(β)＋g(β)，求tan(α＋β)的值．

    查看答案和解析>>

    科目：高中数学 来源：江西省南昌一中、南昌十中2011届高三第一次联考理科数学试题 题型：044

    已知函数f(x)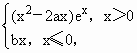＝g(x)＝clnx＋b，且x＝是函数y＝f(x)的极值点．

    (Ⅰ)求实数a的值；

    (Ⅱ)若方程f(x)－m＝0有两个不相等的实数根，求实数m的取值范围；

    (Ⅲ)若直线l是函数y＝f(x)的图象在点(2，f(2))处的切线，且直线l与函数y＝g(x)的图象相切于点P(x0，y0)，x0∈[e－1，e]，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：江苏省扬州中学2012届高三上学期11月练习数学试题 题型：044

    对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)．

    定义：(1)设是函数y＝f(x)的导数的导数，若方程＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”；

    定义：(2)设x0为常数，若定义在R上的函数y＝f(x)对于定义域内的一切实数x，都有f(x0＋x)＋f(x0－x)＝2f(x0)成立，则函数y＝f(x)的图象关于点(x0，f(x0))对称．

    己知f(x)＝x3－2x2＋2，请回答下列问题：

    (1)求函数f(x)的“拐点”A的坐标

    (2)检验函数f(x)的图象是否关于“拐点”A对称，对于任意的三次函数写出一个有关“拐点”的结论(不必证明)

    (3)写出一个三次函数G(x)，使得它的“拐点”是(－1，3)(不要过程)

    查看答案和解析>>

    同步练习册答案