
【题目】已知:2x≤256且log2x≥ ![]() ,
,
(1)求x的取值范围;
(2)求函数log2( ![]() )log2(
)log2( ![]() )的最大值和最小值以及相应的x的取值.
)的最大值和最小值以及相应的x的取值.
【答案】
(1)解:由2x≤256=28,∴x≤8.
且log2x≥ ![]() =
= ![]() ,可得 x≥
,可得 x≥ ![]() .
.
综上可得, ![]() ≤x≤8,即x的范围为[
≤x≤8,即x的范围为[ ![]() ,8]
,8]
(2)解:由(1)可得, ![]() ≤x≤8,∴
≤x≤8,∴ ![]() ≤log2x≤3,
≤log2x≤3,
∴f(x)=(log2x﹣1)(log2x﹣2)= ![]() ﹣
﹣ ![]() ,
,
∴当 log2x= ![]() 时,函数f(x)取得最小值为﹣
时,函数f(x)取得最小值为﹣ ![]() ,此时,x=2
,此时,x=2 ![]() .
.
当 log2x=3时,函数f(x)取得最大值为2,此时x=8
【解析】(1)由2x≤256求得x≤8,再由log2x≥ ![]() 求得 x≥
求得 x≥ ![]() ,综上可得x的范围.(2)由(1)可得,
,综上可得x的范围.(2)由(1)可得, ![]() ≤x≤8,
≤x≤8, ![]() ≤log2x≤3,再根据f(x)=(log2x﹣1)(log2x﹣2),利用二次函数的性质求得它的最值,以及此时对应的x值.
≤log2x≤3,再根据f(x)=(log2x﹣1)(log2x﹣2),利用二次函数的性质求得它的最值,以及此时对应的x值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3位进行其他方面的排查,其中患胃病的人数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
参考公式: 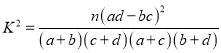 ,其中
,其中![]() .
.
下面的临界值仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知X和Y是两个分类变量,由公式K2= ![]() 算出K2的观测值k约为7.822根据下面的临界值表可推断( )
算出K2的观测值k约为7.822根据下面的临界值表可推断( )
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.推断“分类变量X和Y没有关系”犯错误的概率上界为0.010
B.推断“分类变量X和Y有关系”犯错误的概率上界为0.010
C.有至少99%的把握认为分类变量X和Y没有关系
D.有至多99%的把握认为分类变量X和Y有关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1:已知正方形ABCD的边长是2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A.设点M经过的路程为x,△ABM的面积为S. 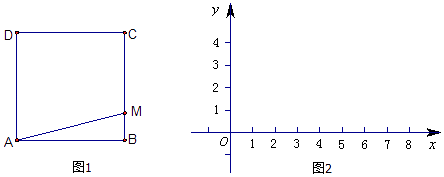
(1)求函数S=f(x)的解析式及其定义域;
(2)在图2中画出函数S=f(x)的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|lnx|,若函数g(x)=f(x)﹣ax在区间(0,3]上有三个零点,则实数a的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,e)
,e)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
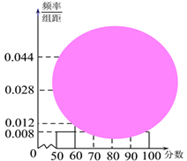
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图:
![]() 求分数在
求分数在![]() 的频率及全班人数;
的频率及全班人数;
![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com