
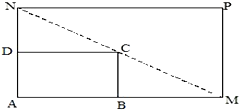
 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=2米,AD=1米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=2米,AD=1米.| 4 |
| x |
| x |
| 2+x |
| 1 |
| AN |
| 2+x |
| x |
| (2+x)2 |
| x |
| (2+x)2 |
| x |
| (2+x)2 |
| x |
| 4 |
| x |
| 25 |
| 3 |
| k |
| x |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2012-2013学年浙江省绍兴市高一下学期期中考试理科数学试卷(解析版) 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为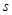 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)

(1)试将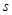 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积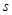 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省绍兴市高一下学期期中考试文科数学试卷(解析版) 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)

(1)试将 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积 取得最大值.
取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com