
【题目】口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
【答案】(1)![]() ;(2)游戏规则不公平,理由见解析.
;(2)游戏规则不公平,理由见解析.
【解析】
试题分析:(1)相当于两人掷含有![]() 个面的色子,共
个面的色子,共![]() 种情况,然后输入和为偶数,且和为
种情况,然后输入和为偶数,且和为![]() 的情况种数,然后用古典概型求概率;(2)偶数,就是甲胜,其他情况乙胜,分别算出甲胜的概率和乙胜的概率,比较是否相等,相等就公平,不相等就不公平.
的情况种数,然后用古典概型求概率;(2)偶数,就是甲胜,其他情况乙胜,分别算出甲胜的概率和乙胜的概率,比较是否相等,相等就公平,不相等就不公平.
试题解析:解:(1)设“甲胜且编号的和为6”为事件![]() .
.
甲编号为![]() ,乙编号为
,乙编号为![]() ,
,![]() 表示一个基本事件,
表示一个基本事件,
则两人摸球结果包括(1,2),(1,3),…,(1,5),(2,1),(2,2),…,(5,4),(5,5)共25个基本事件;
![]() 包括的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1)共5个.
包括的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1)共5个.
∴![]() .
.
答:甲胜且编号的和为6的事件发生的概率为![]() .
.
(2)这种游戏不公平.
设“甲胜”为事件![]() ,“乙胜”为事件
,“乙胜”为事件![]() .甲胜即两个编号的和为偶数所包含基本事件数为以下13个:(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).
.甲胜即两个编号的和为偶数所包含基本事件数为以下13个:(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).
所以甲胜的概率为![]() ,乙胜的概率为
,乙胜的概率为![]() ,
,
∵![]() ,∴这种游戏规则不公平.
,∴这种游戏规则不公平.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,直线
,直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,且分别交椭圆于
,且分别交椭圆于![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三数学奥林匹克竞赛集训队的一次数学测试成绩的茎叶图(图1)和频率分布直方图(图2)都受到不同程度的破坏,可见部分如图所示,据此解答如下问题.
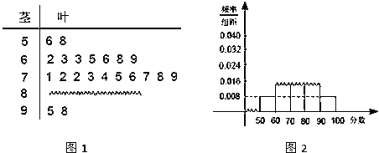
(1)求该集训队总人数及分数在[80,90)之间的频数;
(2)计算频率分布直方图中[80,90)的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生的答题情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
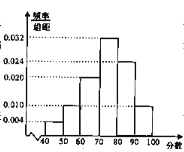
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
,![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]()
![]() ,
,![]() ,则
,则![]() 为常函数;
为常函数;
④若多面体![]() 的体积
的体积![]() ,
,![]() ,则
,则![]() 为单调函数.
为单调函数.
其中假命题为( )
A.① ③ B.② C.③④ D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com