分析:(Ⅰ)先根据线面垂直的判定定理可知B
1C
1⊥平面A
1B
1D,再根据线面垂直的性质可知B
1C
1⊥B
1E,B
1E⊥A
1D,则B
1E是异面直线B
1C
1与A
1D的公垂线,利用等面积法求出B
1E的长;
(Ⅱ)根据BC∥B
1C
1,可得BC⊥平面ABDE,从而BC为四棱锥C-ABDE的高.从而所求四棱锥的体积V为V=V
C-ABDE=
×BC×S,其中S为四边形ABDE的面积,过E作EF⊥BD,垂足为F.利用等面积法求出EF,而S=S
△A1AE-S
△A1AE-S
△A1B1D即可求出所求.
解答:解:(Ⅰ)由直三棱柱的定义知B
1C
1⊥B
1D,又因为∠ABC=90°,
因此B
1C
1⊥A
1B
1,从而B
1C
1⊥平面A
1B
1D,得B
1C
1⊥B
1E.又B
1E⊥A
1D,
故B
1E是异面直线B
1C
1与A
1D的公垂线
由
BD=BB1知
B1D=,
在Rt△A
1B
1D中,A
2D=
==.
又因
S△A1B1D=A1B1•B1D=A1D•B1E.
故B
1E=
==.
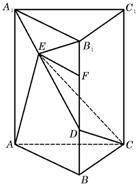
(Ⅱ)由(Ⅰ)知B
1C
1⊥平面A
1B
1D,又BC∥B
1C
1,故BC⊥平面ABDE,
即BC为四棱锥C-ABDE的高.从而所求四棱锥的体积V为
V=V
C-ABDE=
×BC×S,
其中S为四边形ABDE的面积.如图1,过E作EF⊥BD,垂足为F.
在Rt△B
1ED中,ED=
==,
又因S
△B1ED=
B1E?DE=B1D?EF,
故EF=
=.
因△A
1AE的边A
1A上的高
h=A1B1-EF=1-=,故
S
△A1AE=
A1A?h=•2•=.
又因为S
△A1BD=
A1B1•B1D=•2•=,从而
S=S
△A1AE-S
△A1AE-S
△A1B1D=2-
-=.
所以
V=?S?BC=••=.
点评:本题主要考查了异面直线的距离,以及三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

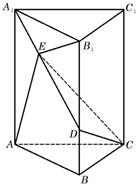 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=1,BC=
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=1,BC= (Ⅱ)由(Ⅰ)知B1C1⊥平面A1B1D,又BC∥B1C1,故BC⊥平面ABDE,
(Ⅱ)由(Ⅰ)知B1C1⊥平面A1B1D,又BC∥B1C1,故BC⊥平面ABDE,

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案



