
函数y=f′(x)是函数y=f(x)的导函数,且函数y=f(x)在点P(x0,f(x0))处的切线为l:y=g(x)=f′(x0)·(x-x0)+f(x0),F(x)=f(x)-g(x), 如果函数y=f(x)在区间[a,b]上的图象如图所示,且a<x0<b,那么( )
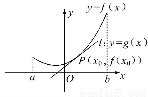
(A)F'(x0)=0,x=x0是F(x)的极大值点
(B)F'(x0)=0,x=x0是F(x)的极小值点
(C)F'(x0)≠0,x=x0不是F(x)的极值点
(D)F'(x0)≠0,x=x0是F(x)的极值点
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
一个空间几何体的三视图如图所示,则该几何体的体积为( )
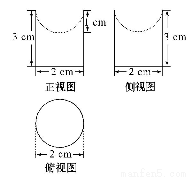
(A) πcm3 (B)3πcm3
πcm3 (B)3πcm3
(C) πcm3 (D)
πcm3 (D) πcm3
πcm3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:解答题
设f(x)=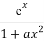 ,其中a为正实数.
,其中a为正实数.
(1)当a= 时,求f(x)的极值点.
时,求f(x)的极值点.
(2)若f(x)为[ ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:选择题
设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则( )
(A)a<-1 (B)a>-1
(C)a>- (D)a<-
(D)a<-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:选择题
根据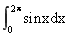 =0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
=0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
(A)面积为0
(B)曲边梯形在x轴上方的面积大于在x轴下方的面积
(C)曲边梯形在x轴上方的面积小于在x轴下方的面积
(D)曲边梯形在x轴上方的面积等于在x轴下方的面积
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:选择题
已知cos(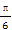 -α)=
-α)= ,则sin(α-
,则sin(α-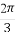 )等于( )
)等于( )
(A) (B)-
(B)- (C)
(C) (D)-
(D)-
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=2sin(2x+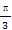 )的图象关于点P(x0,0)对称,若x0∈[-
)的图象关于点P(x0,0)对称,若x0∈[-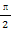 ,0],则x0等于( )
,0],则x0等于( )
(A)-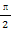 (B)-
(B)-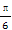 (C)-
(C)- (D)-
(D)-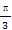
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com