
【题目】已知函数f(x)= ![]() sin2x+cos2(
sin2x+cos2( ![]() ﹣x)﹣
﹣x)﹣ ![]() (x∈R).
(x∈R).
(1)求函数f(x)在区间[0, ![]() ]上的最大值;
]上的最大值;
(2)在△ABC中,若A<B,且f(A)=f(B)= ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:f(x)= ![]() sin2x+cos2(
sin2x+cos2( ![]() ﹣x)﹣
﹣x)﹣ ![]()
= ![]()
![]() +
+ 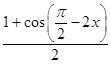 ﹣
﹣ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x
cos2x
=sin(2x﹣ ![]() )
)
由于0≤x≤ ![]() ,因此﹣
,因此﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,所以当2x﹣
,所以当2x﹣ ![]() =
= ![]() 即x=
即x= ![]() 时,f(x)取得最大值,最大值为1
时,f(x)取得最大值,最大值为1
(2)解:由已知,A、B是△ABC的内角,A<B,且f(A)=f(B)= ![]() ,
,
可得:2A﹣ ![]() =
= ![]() ,2B﹣
,2B﹣ ![]() =
= ![]() ,
,
解得A= ![]() ,B=
,B= ![]() ,
,
所以C=π﹣A﹣B= ![]() ,
,
得 ![]()
![]() =
= ![]()
【解析】(1)利用三角恒等变换的应用可化简f(x)=sin(2x﹣ ![]() ),再利用正弦函数的单调性可求函数f(x)在区间[0,
),再利用正弦函数的单调性可求函数f(x)在区间[0, ![]() ]上的最大值;(2)在△ABC中,由A<B,且f(A)=f(B)=
]上的最大值;(2)在△ABC中,由A<B,且f(A)=f(B)= ![]() ,可求得A=
,可求得A= ![]() ,B=
,B= ![]() ,再利用正弦定理即可求得
,再利用正弦定理即可求得 ![]() 的值.
的值.
【考点精析】掌握三角函数的最值是解答本题的根本,需要知道函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足acosB=bcosA.
(1)判断△ABC的形状;
(2)求sin(2A+ ![]() )﹣2cos2B的取值范围.
)﹣2cos2B的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解不等式( ![]() )x﹣x+
)x﹣x+ ![]() >0时,可构造函数f(x)=(
>0时,可构造函数f(x)=( ![]() )x﹣x,由f(x)在x∈R是减函数,及f(x)>f(1),可得x<1.用类似的方法可求得不等式arcsinx2+arcsinx+x6+x3>0的解集为( )
)x﹣x,由f(x)在x∈R是减函数,及f(x)>f(1),可得x<1.用类似的方法可求得不等式arcsinx2+arcsinx+x6+x3>0的解集为( )
A.(0,1]
B.(﹣1,1)
C.(﹣1,1]
D.(﹣1,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 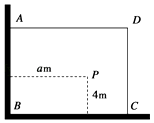
A.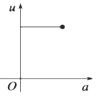
B.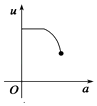
C.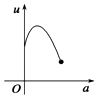
D.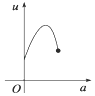
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱柱ABCD﹣A1B1C1D1 , AB=a,AA1=2a,E,F分别是棱AD,CD的中点.
(1)求异面直线BC1与EF所成角的大小;
(2)求四面体CA1EF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C是平面内到直线l1:x=﹣1和直线l2:y=1的距离之积等于常数k2(k>0)的点的轨迹,下列四个结论:
①曲线C过点(﹣1,1);
②曲线C关于点(﹣1,1)成中心对称;
③若点P在曲线C上,点A、B分别在直线l1、l2上,则|PA|+|PB|不小于2k;
④设P0为曲线C上任意一点,则点P0关于直线l1:x=﹣1,点(﹣1,1)及直线f(x)对称的点分别为P1、P2、P3 , 则四边形P0P1P2P3的面积为定值4k2;其中,
所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 ![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ= ![]() ,0°<θ<90°)且与点A相距10
,0°<θ<90°)且与点A相距10 ![]() 海里的位置C. (Ⅰ)求该船的行驶速度(单位:海里/小时);
海里的位置C. (Ⅰ)求该船的行驶速度(单位:海里/小时);
(Ⅱ)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,平面BDEF⊥平面ABCD,四边形BDEF是正方形,点M在线段EF上, ![]() =λ
=λ ![]() .
. 
(1)当λ= ![]() ,求证:BM∥平面ACE;
,求证:BM∥平面ACE;
(2)如二面角A﹣BM﹣C的平面角的余弦值为﹣ ![]() ,求实数λ的值.
,求实数λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com