Question

我们用min｛S₁，S₂，…，S_n｝和max｛S₁，S₂，…，S_n｝分别表示实数S₁，S₂，…，S_n中的最小者和最大者．

(1)设f(x)＝min｛sinx，cosx｝，g(x)＝max｛sinx，cosx｝，x∈［0，2π］，函数f(x)的值域为A，函数g(x)的值域为B，求A∩B；

(2)数学课上老师提出了下面的问题：设a₁，a₂，a_n为实数，x∈R，求函数(x₁＜x₂＜x_n∈R＝的最小值或最大值．为了方便探究，遵循从特殊到一般的原则，老师让学生先解决两个特例：求函数和的最值．学生甲得出的结论是：［f(x)］_min＝min｛f(－2)，f(－1)，f(1)｝，且f(x)无最大值．学生乙得出的结论是：［g(x)］_max＝max｛g(－1)，g(1)，g(2)｝，且g(x)无最小值．请选择两个学生得出的结论中的一个，说明其成立的理由；

(3)试对老师提出的问题进行研究，写出你所得到的结论并加以证明(如果结论是分类的，请选择一种情况加以证明)．

Answer 1

答案：
解析：

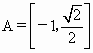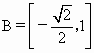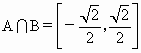　　(1)，，∴．　　4分

　　(2)若选择学生甲的结论，则说明如下，

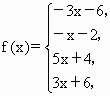
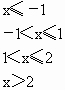　　，于是在区间上是减函数，在上是减函数，在上是增函数，在上是增函数．　　8分

　　所以函数的最小值是，且函数没有最大值．　　10分

　　若选择学生乙的结论，则说明如下，

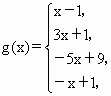
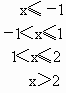　　，于是在区间上是增函数，在上是增函数，在上是减函数，在上是减函数．

　　所以函数的最大值是，且函数没有最小值．　　10分(3)结论：

　　若，则；

　　若，则；

　　若，则，

　　

　　(写出每个结论得1分，共3分，证明为5分)

　　以第一个结论为例证明如下：

　　∵，∴当时，

　　，是减函数，

　　当时，

　　，是增函数

　　当时，函数的图像是以点，，

　　为端点的一系列互相连接的折线所组成，

　　所以有．