
【题目】学生考试中答对但得不了满分的原因多为答题不规范,具体表现为:解题结果正确,无明显推理错误,但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等,记此类解答为“![]() 类解答”为评估此类解答导致的失分情况,某市教研室做了项试验:从某次考试的数学试卷中随机抽取若干属于“
类解答”为评估此类解答导致的失分情况,某市教研室做了项试验:从某次考试的数学试卷中随机抽取若干属于“![]() 类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
教师评分(满分12分) | 11 | 10 | 9 |
各分数所占比例 |
|
|
|
某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两名老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于等于1分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于1分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分;当一、二评分数和仲裁分数差值的绝对值相同时,取仲裁分数和前两评中较高的分数的平均分为该题得分.(假设本次考试阅卷老师对满分为12分的题目中的“![]() 类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
(1)本次数学考试中甲同学某题(满分12分)的解答属于“![]() 类解答”,求甲同学此题得分
类解答”,求甲同学此题得分![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)本次数学考试有6个解答题,每题满分12分,同学乙6个题的解答均为“![]() 类解答”.
类解答”.
①记乙同学6个题得分为![]() 的题目个数为
的题目个数为![]() 计算事件
计算事件![]() 的概率.
的概率.
②同学丙的前四题均为满分,第5题为“![]() 类解答”,第6题得8分.以乙、丙两位同学解答题总分均值为依据,谈谈你对“
类解答”,第6题得8分.以乙、丙两位同学解答题总分均值为依据,谈谈你对“![]() 类解答”的认识.
类解答”的认识.
【答案】(1)分布列见解析,![]() ;(2)①
;(2)①![]() ;②见解析.
;②见解析.
【解析】
(1)根据题意,随机变量![]() 的取值为9,9.5,10,10.5,11 ,再分析一评、二评、仲裁所打的分数情况,然后根据相互独立事件的概率逐一求出相应的概率,得到分布列,求得数学期望;
的取值为9,9.5,10,10.5,11 ,再分析一评、二评、仲裁所打的分数情况,然后根据相互独立事件的概率逐一求出相应的概率,得到分布列,求得数学期望;
(2)①方法一:事件“![]() ”可分为
”可分为![]() ;
;![]() ;
;![]() ;
;![]() 四种情况,结合独立事件的概率计算公式,求得概率;
四种情况,结合独立事件的概率计算公式,求得概率;
方法二:记“![]() 或
或![]() ”为事件
”为事件![]() ,6次实验中,事件
,6次实验中,事件![]() 发生的次数
发生的次数![]() ,“
,“![]() ”相当于事件
”相当于事件![]() 恰好发生3次,结合独立重复试验的概率计算公式求解;
恰好发生3次,结合独立重复试验的概率计算公式求解;
②依次求出乙丙的数学期望,通过比较数学期望值的大小,即可得到结论.
(1)根据题意,随机变量![]() 的取值为9,9.5,10,10.5,11
的取值为9,9.5,10,10.5,11
设一评、二评、仲裁所打的分数分别是![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
故![]() 的分布列为
的分布列为
| 9 | 9.5 | 10 | 10.5 | 11 |
|
|
|
|
|
|
![]()
(2)①方法一
事件“![]() ”可分为
”可分为![]() ;
;![]() ;
;![]() ;
;![]() 四种情况,其概率为
四种情况,其概率为![]()
![]() .
.
方法二
记“![]() 或
或![]() ”为事件
”为事件![]() ,6次实验中,事件
,6次实验中,事件![]() 发生的次数
发生的次数![]() ,“
,“![]() ”相当于事件
”相当于事件![]() 恰好发生3次,故概率为:
恰好发生3次,故概率为:![]() .
.
②由题意可知:乙同学得分的均值为![]() ,
,
丙同学得分的均值为:![]() .
.
显然,丙同学得分均值更高,所以“会而不对”和不会做一样都会丢分,在做题过程中要规范作答,尽量避免“![]() 类解答”的出现.
类解答”的出现.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
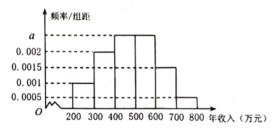
①样本数据落在区间![]() 的频率为0.45;
的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有初中学生1800人,高中学生1200人,为了解学生本学期课外阅读时间,现采用分成抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.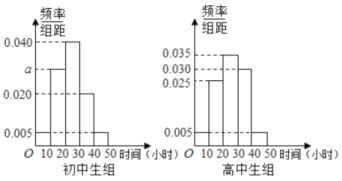
(1)写出![]() 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(2)从阅读时间不足10个小时的样本学生中随机抽取3人,并用![]() 表示其中初中生的人数,求
表示其中初中生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
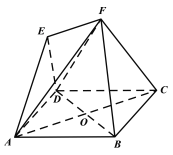
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在求出
,若存在求出![]() 的长,若不存在说明理由.
的长,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生![]() 人,学号为
人,学号为![]() ,
,![]() ,
,![]() ,
,![]() ;女生
;女生![]() 人,学号为
人,学号为![]() ,
,![]() ,
,![]() ,
,![]() .对高三学生进行问卷调查,按学号采用系统抽样的方法,从这
.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这![]() 名学生中抽取
名学生中抽取![]() 人进行问卷调查(第一组采用简单随机抽样,抽到的号码为
人进行问卷调查(第一组采用简单随机抽样,抽到的号码为![]() );再从这
);再从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人进行数据分析,则这
人进行数据分析,则这![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图一所示,四边形![]() 是边长为
是边长为![]() 的正方形,沿
的正方形,沿![]() 将
将![]() 点翻折到
点翻折到![]() 点位置(如图二所示),使得二面角
点位置(如图二所示),使得二面角![]() 成直二面角.
成直二面角.![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
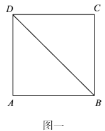
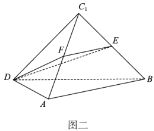
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com