
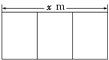
ЁОЬтФПЁП ЮЊСЫОЛЛЏЙужнЫЎЯЕЃЌФтдкаЁЧхКгНЈвЛзљЦНУцЭМ(ШчЭМЫљЪО)ЮЊОиаЮЧвУцЛ§ЮЊ200 m2ЕФШ§МЖЮлЫЎДІРэГиЃЌгЩгкЕиаЮЯожЦЃЌГЄЁЂПэЖМВЛФмГЌЙ§16 mЃЌШчЙћГиЭтБкНЈдьЕЅМлЮЊ400дЊ/m2ЃЌжаМфСНЬѕИєЧННЈдьЕЅМлЮЊ248дЊ/m2ЃЌГиЕзНЈдьЕЅМлЮЊ80дЊ/m2(ГиБкКёЖШКіТдВЛМЦЃЌЧвГиЮоИЧ)ЃЎ
(1)аДГізмдьМлy(дЊ)гыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіЖЈвхгђЃЛ
(2)ЧѓЮлЫЎДІРэГиЕФГЄКЭПэИїЮЊЖрЩйЪБЃЌЮлЫЎДІРэГиЕФзмдьМлзюЕЭЃЌВЂЧѓзюЕЭдьМлЃЎ
ЁОД№АИЁП(1) yЃН800xЃЋ![]() ЃЋ16 000ЃЌ
ЃЋ16 000ЃЌ![]() ЁмxЁм16.
ЁмxЁм16.
(2) ЕБГЄЮЊ16 mЃЌПэЮЊ12.5 mЪБЃЌзмдьМлyзюЕЭЃЌЮЊ45 000дЊЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЯШЧѓУцЛ§ЃЌдйГЫвдЖдгІМлИёЃЌЧѓКЭЕУзмдьМлЃЌИљОнГЄЁЂПэЖМВЛФмГЌЙ§16 mвЊЧѓШЗЖЈЖЈвхгђЃЈ2ЃЉРћгУЕМЪ§ПЩЕУКЏЪ§ЮЊЖЈвхгђЩЯЕЅЕїМѕКЏЪ§ЃЌдйИљОнЕЅЕїадЧѓзюаЁжЕ
ЪдЬтНтЮіЃКНтЃК(1)ОиаЮЦНУцЭМЕФСНБпГЄЗжБ№ЮЊx mЃЌ![]() mЃЌ
mЃЌ
ИљОнЬтвтЃЌЕУ
НтЕУ![]() ЁмxЁм16.
ЁмxЁм16.
yЃН![]() ЁС400ЃЋ
ЁС400ЃЋ![]() ЁС248ЃЋ16 000
ЁС248ЃЋ16 000
ЃН800xЃЋ![]() ЃЋ16 000ЃЌ
ЃЋ16 000ЃЌ![]() ЁмxЁм16.
ЁмxЁм16.
(2)yЁфЃН800Ѓ![]() ЃЌ
ЃЌ
ЕБ![]() ЁмxЁм16ЪБЃЌyЁфЃМ0ЃЌКЏЪ§дк
ЁмxЁм16ЪБЃЌyЁфЃМ0ЃЌКЏЪ§дк![]() ЩЯЮЊМѕКЏЪ§ЃЌ
ЩЯЮЊМѕКЏЪ§ЃЌ
ЫљвдЕБГЄЮЊ16 mЃЌПэЮЊ12.5 mЪБЃЌзмдьМлyзюЕЭЃЌЮЊ45 000дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНlogaЃЈxЉ1ЃЉЃЈaЃО0ЃЌЧвaЁй1ЃЉЃЎ
ЃЈ1ЃЉШєfЃЈxЃЉдк[2ЃЌ9]ЩЯЕФзюДѓжЕгызюаЁжЕжЎВюЮЊ3ЃЌЧѓaЕФжЕЃЛ
ЃЈ2ЃЉШєaЃО1ЃЌЧѓВЛЕШЪНfЃЈ2xЃЉЃО0ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮхУцЬх![]() жаЃЌЫФБпаЮ
жаЃЌЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ ![]() ЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮЃЌ
ЪЧБпГЄЮЊ2ЕФе§Ш§НЧаЮЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
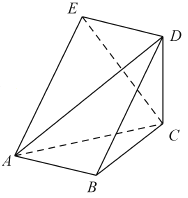
ЃЈ1ЃЉжЄУїЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() дкЦНУц
дкЦНУц![]() ФкЕФе§ЭЖгАЮЊ
ФкЕФе§ЭЖгАЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕНЦНУц
ЕНЦНУц![]() ЕФОрРыЃЎ
ЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЯђСП![]() ЃЌ
ЃЌ![]() ЃЌдђЯТСаа№ЪіДэЮѓЕФЪЧ( )
ЃЌдђЯТСаа№ЪіДэЮѓЕФЪЧ( )
A.Шє![]() ЪБЃЌдђ
ЪБЃЌдђ![]() гы
гы![]() ЕФМаНЧЮЊЖлНЧ
ЕФМаНЧЮЊЖлНЧ
B.![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]()
C.гы![]() ЙВЯпЕФЕЅЮЛЯђСПжЛгавЛИіЮЊ
ЙВЯпЕФЕЅЮЛЯђСПжЛгавЛИіЮЊ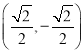
D.Шє![]() ЃЌдђ
ЃЌдђ![]() Лђ
Лђ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌЦфЧуаБНЧЮЊ
ЃЌЦфЧуаБНЧЮЊ![]() ЃЌдквддЕу
ЃЌдквддЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЗЧИКАыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЈШЁЯрЭЌЕФГЄЖШЕЅЮЛЃЉЃЌЧњЯп
жсЗЧИКАыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЈШЁЯрЭЌЕФГЄЖШЕЅЮЛЃЉЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]()
ЃЈЂёЃЉШєжБЯп![]() гыЧњЯп
гыЧњЯп![]() гаЙЋЙВЕуЃЌЧѓ
гаЙЋЙВЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂђЃЉЩш![]() ЮЊЧњЯп
ЮЊЧњЯп![]() ЩЯШЮвтвЛЕуЃЌЧѓ
ЩЯШЮвтвЛЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЩшКЏЪ§f(x)ЃН(xЃ1)2ЃЋbln xЃЌЦфжаbЮЊГЃЪ§ЃЎ
(1)ЕБb>![]() ЪБЃЌХаЖЯКЏЪ§f(x)дкЖЈвхгђЩЯЕФЕЅЕїадЃЛ
ЪБЃЌХаЖЯКЏЪ§f(x)дкЖЈвхгђЩЯЕФЕЅЕїадЃЛ
(2)ШєКЏЪ§f(x)гаМЋжЕЕуЃЌЧѓbЕФШЁжЕЗЖЮЇМАf(x)ЕФМЋжЕЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЏЕу![]() ЕНЖЈжБЯп
ЕНЖЈжБЯп![]() ЃК
ЃК![]() ЕФОрРыБШЕНЖЈЕу
ЕФОрРыБШЕНЖЈЕу![]() ЕФОрРыДѓ2.
ЕФОрРыДѓ2.
ЃЈ1ЃЉЧѓЖЏЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉдк![]() жсе§АыжсЩЯЃЌЪЧЗёДцдкФГИіШЗЖЈЕФЕу
жсе§АыжсЩЯЃЌЪЧЗёДцдкФГИіШЗЖЈЕФЕу![]() ЃЌЙ§ИУЕуЕФЖЏжБЯп
ЃЌЙ§ИУЕуЕФЖЏжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЪЙЕУ
СНЕуЃЌЪЙЕУ![]() ЮЊЖЈжЕ.ШчЙћДцдкЃЌЧѓГіЕу
ЮЊЖЈжЕ.ШчЙћДцдкЃЌЧѓГіЕу![]() зјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
зјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк5МўВњЦЗжаЃЌга3МўвЛЕШЦЗКЭ2МўЖўЕШЦЗЃЌДгжаШЮШЁ2МўЃЌвд![]() ЮЊИХТЪЕФЪТМўЪЧ(ЁЁЁЁ)
ЮЊИХТЪЕФЪТМўЪЧ(ЁЁЁЁ)
A. ЧЁга1МўвЛЕШЦЗ B. жСЩйгавЛМўвЛЕШЦЗ
C. жСЖргавЛМўвЛЕШЦЗ D. ЖМВЛЪЧвЛЕШЦЗ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЧAЃЌBЃЌCЫљЖдЕФБпЗжБ№ЮЊaЃЌbЃЌcЃЌЧвaЃЋbЃЋcЃН8.
(1)ШєaЃН2ЃЌbЃН![]() ЃЌЧѓcosCЕФжЕЃЛ
ЃЌЧѓcosCЕФжЕЃЛ
(2)ШєsinAcos2![]() ЃЋsinBЁЄcos2
ЃЋsinBЁЄcos2![]() ЃН2sinCЃЌЧвЁїABCЕФУцЛ§SЃН
ЃН2sinCЃЌЧвЁїABCЕФУцЛ§SЃН![]() sinCЃЌЧѓaКЭbЕФжЕЃЎ
sinCЃЌЧѓaКЭbЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com