Question

【题目】给出集合.

（1）若，求证：函数；

（2）由（1）分析可知， 是周期函数且是奇函数，于是张三同学得出两个命

题：命题甲：集合中的元素都是周期函数.命题乙：集合中的元素都是奇函数. 请对此

给出判断，如果正确，请证明；如果不正确，请举反例；

（3）若，数列满足： ，且 ，数列的前项

和为，试问是否存在实数、，使得任意的，都有成立，若

存在，求出、的取值范围，若不存在，说明理由.

Answer 1

【答案】（1）见解析（2）命题甲正确（3）

【解析】试题分析：

(1)原问题即，结合两角和差正余弦公式整理变形即可证得题中的结论；

(2)由题意可得：命题甲正确. 集合中的元素都是周期为6的周期函数.命题乙不正确.如是奇函数； 不是奇函数.

(3)由题意可得，假设存在实数满足题设，据此计算可得，即数列是周期为的周期数列，且前6项依次为，据此可知，则满足题意时只需即可.

试题解析：

（1）转化证明

左边

右边

（2）命题甲正确. 集合中的元素都是周期为6的周期函数.

验证即可

命题乙不正确.集合中的元素不都是奇函数.

如是奇函数； 不是奇函数.

（3） ，则

假设存在实数满足题设，则

所以数列是周期为的周期数列，且前6项依次为

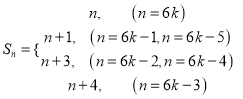
当， 时，

当 时，

当 时，

当 时，

综上

要使对任意的，都有恒成立，

只要即可.