
【题目】若f(x)=x2﹣x+b,且f(log2a)=b,log2[f(a)]=2(a≠1).
(1)求f(log2x)的最小值及对应的x值;
(2)x取何值时,f(log2x)>f(1)且log2[f(x)]<f(1)?
【答案】
(1)解:∵f(x)=x2﹣x+b,∴f(log2a)=log22a﹣log2a+b.
由已知有log22a﹣log2a+b=b,∴(log2a﹣1)log2a=0.
∵a≠1,∴log2a=1.∴a=2.
又log2[f(a)]=2,∴f(a)=4.
∴a2﹣a+b=4,b=4﹣a2+a=2.
故f(x)=x2﹣x+2,从而f(log2x)=log22x﹣log2x+2=(log2x﹣ ![]() )2+
)2+ ![]() .
.
∴当log2x= ![]() 即x=
即x= ![]() 时,f(log2x)有最小值
时,f(log2x)有最小值 ![]()
(2)解:由题意 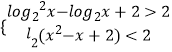
![]() 0<x<1
0<x<1
【解析】(1)把log2a代入f(x)中,解关于log2a的一元二次方程,求出a的值;再把f(a)的值代入log2[f(a)]=2中,求出b的值;从而确定函数f(x)的解析式;把log2x代入函数f(x)中,配方法求f(log2x)的最小值及对应的x值;(2)利用对数恒等式和对数函数的单调性解不等式.


科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,是否存在整数
时,是否存在整数![]() ,使不等式
,使不等式![]() 恒成立?若存在,求整数
恒成立?若存在,求整数![]() 的值;若不存在,则说明理由;
的值;若不存在,则说明理由;
(3)关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( ) 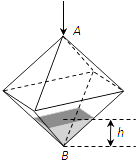
A.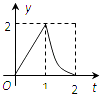
B.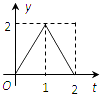
C.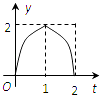
D.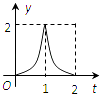
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知 ![]() 在区间(m2﹣4m,2m﹣2)上能取得最大值,求实数m的取值范围;
在区间(m2﹣4m,2m﹣2)上能取得最大值,求实数m的取值范围;
(2)设函数f(x)=ax﹣(k﹣1)a﹣x(a>0且a≠1)是定义域为R的奇函数,若 ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校游园活动有这样一个游戏:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除了颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
(1)求在1次游戏中:
①摸出3个白球的概率.
②获奖的概率.
(2)求在3次游戏中获奖次数X的分布列.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com