
【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附: ![]()
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)分析,你认为选派哪位学生参加合适?请说明理由
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD,
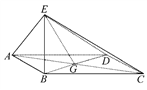
(1)证明:平面AEC⊥平面BED.
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为![]() ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为![]() .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点且
两点且![]() ,是否存在以原点
,是否存在以原点![]() 为圆心的定圆与直线
为圆心的定圆与直线![]() 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中, ![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 是抛物线
是抛物线![]() 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过![]() 三点的圆的圆心为
三点的圆的圆心为![]() ,点
,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]()
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]()
![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() ,求当
,求当![]() 时,
时, ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com