
【题目】已知椭圆C: ![]() (a>b>0)的焦距为
(a>b>0)的焦距为![]() ,且椭圆C过点A(1,
,且椭圆C过点A(1, ![]() ),
),
(Ⅰ)求椭圆C的方程;
(Ⅱ)若O是坐标原点,不经过原点的直线L:y=kx+m与椭圆交于两不同点P(x1,y1),Q(x2,y2),且y1y2=k2x1x2,求直线L的斜率k;
(Ⅲ)在(Ⅱ)的条件下,求△OPQ面积的最大值.
【答案】(I)![]() ;(Ⅱ)斜率为
;(Ⅱ)斜率为![]() 或﹣
或﹣![]() ;(Ⅲ)1.
;(Ⅲ)1.
【解析】试题分析:(1)由椭圆的焦距为![]() ,且椭圆C过点A(1,
,且椭圆C过点A(1, ![]() ),列出方程求出a,b,由此能求出椭圆C的方程.
),列出方程求出a,b,由此能求出椭圆C的方程.
(2)由![]() ,得: (1+4k2)x2+8kmx+4(m2﹣1)=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的斜率.
,得: (1+4k2)x2+8kmx+4(m2﹣1)=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的斜率.
(3)把直线方程![]() 与椭圆方程
与椭圆方程![]() 联立,得: x2+2mx+2m2﹣2=0,,由此利用根的判别式、韦达定理、点到直线距离公式、弦长公式能求出△OPQ 面积的最大值.
联立,得: x2+2mx+2m2﹣2=0,,由此利用根的判别式、韦达定理、点到直线距离公式、弦长公式能求出△OPQ 面积的最大值.
试题解析:
(Ⅰ)∵椭圆C: ![]() 的焦距为
的焦距为![]() ,且椭圆C过点
,且椭圆C过点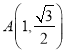 ,
,
∴由题意得![]() ,可设椭圆方程为
,可设椭圆方程为![]() ,
,
则![]() ,得
,得![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)由![]() 消去y得:(1+4k2)x2+8kmx+4(m2﹣1)=0,
消去y得:(1+4k2)x2+8kmx+4(m2﹣1)=0,
△=64k2m2﹣16(1+4k2)(m2﹣1)=16(4k2﹣m2+1)>0,
![]() ,
,
故![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵m≠0,∴![]() ,解得
,解得![]() ,
,
∴直线L的斜率为![]() 或﹣
或﹣![]() .
.
(Ⅲ)由(Ⅱ)可知直线L的方程为![]()
由对称性,不妨把直线方程![]() 与椭圆方程
与椭圆方程![]() 联立,消去y得:2x2+4mx+4m2﹣4=0,△=64m2﹣4(4m2﹣4)>0,∵P(x1,y1),Q(x2,y2),∴x1+x2=﹣2m,
联立,消去y得:2x2+4mx+4m2﹣4=0,△=64m2﹣4(4m2﹣4)>0,∵P(x1,y1),Q(x2,y2),∴x1+x2=﹣2m, ![]() ,
,
设d为点O到直线l的距离,则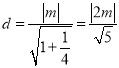 ,
,
![]()
当且仅当m2=1时,等号成立.∴△OPQ面积的最大值为1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】
一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为![]() .
.
(1)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(2)求“抽取的卡片上的数字![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,抛物线上一点
,抛物线上一点![]() 的横坐标为1,且到焦点
的横坐标为1,且到焦点![]() 的距离为2.
的距离为2.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 是抛物线上异于原点
是抛物线上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别为
的倾斜角分别为![]() 和
和![]() ,当
,当![]() 变化且
变化且![]() 为定值
为定值![]() 时,证明直线
时,证明直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2010年至2016年农村居民家庭纯收入![]() (单位:千元)的数据如下表
(单位:千元)的数据如下表
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程。
的线性回归方程。
(2)判断![]() 与
与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2018年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
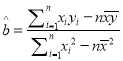 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,若存在实数
,若存在实数![]() 使得一条曲线与直线
使得一条曲线与直线![]() 由两个不同的交点,且以这两个交点为端点的线段长度恰好等于
由两个不同的交点,且以这两个交点为端点的线段长度恰好等于![]() ,则称此曲线为直线
,则称此曲线为直线![]() 的“绝对曲线”.下面给出的四条曲线方程:
的“绝对曲线”.下面给出的四条曲线方程:
①![]() ;②
;② ![]() ;③
;③![]() ;④
;④![]() .
.
其中直线![]() 的“绝对曲线”的条数为( )
的“绝对曲线”的条数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某折叠餐桌的使用步骤如图所示,有如图检查项目:
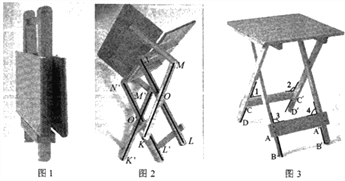
项目①:折叠状态下(如图1),检查四条桌腿长相等;
项目②:打开过程中(如图2),检查![]() ;
;
项目③:打开过程中(如图2),检查![]() ;
;
项目④:打开后(如图3),检查![]() ;
;
项目⑤:打开后(如图3),检查![]() .
.
在检查项目的组合中,可以正确判断“桌子打开之后桌面与地面平行的是”( )
A. ①②③ B. ②③④ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在一个等比数列{an}同时满足下列三个条件:①a1+a6=11且a3a4= ![]() ;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得
;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得 ![]() am﹣1 , am2 , am+1+
am﹣1 , am2 , am+1+ ![]() 依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com