
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
,![]() 是边长为
是边长为![]() 的正三角形,求直线
的正三角形,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
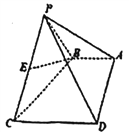
【答案】(1)见解析;(2)![]()
【解析】分析:(1)证线面平行只需在面内找一线与已知线平行即可,取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]()
证四边形![]() 为平行四边形即可;(2)求线面角先找出线面角是关键,取
为平行四边形即可;(2)求线面角先找出线面角是关键,取![]() 的中点
的中点![]() ,连结
,连结![]() ,证明
,证明![]() 平面
平面![]() ,记点
,记点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,根据等体积法求出h,三棱锥
,根据等体积法求出h,三棱锥![]() 的体积
的体积![]() ,再结合
,再结合![]() 即可得出.
即可得出.
详解:
(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,且
,且![]()
又∵![]() ,且
,且![]()
∴![]() ,且
,且![]() ,故四边形
,故四边形![]() 为平行四边形
为平行四边形
∴![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
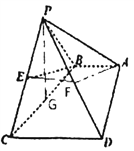
(2)取![]() 的中点
的中点![]() ,连结
,连结![]()
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
又![]() 是边长为
是边长为![]() 的正三角形
的正三角形
∴![]() ,
,![]() ,且
,且![]()
∵平面![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
∵四边形是直角梯形,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
记点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵三棱锥![]() 的体积
的体积![]()
∴![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)的图象关于y轴对称,且f(x)在[0,+∞)上单调递减,若关于x的不等式f(2mx﹣lnx﹣3)≥2f(3)﹣f(﹣2mx+lnx+3)在x∈[1,3]上恒成立,则实数m的取值范围为( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() ,则下列说法正确的是__________.(写出所有正确结论的序号)
,则下列说法正确的是__________.(写出所有正确结论的序号)
①![]() 是偶函数;
是偶函数;
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③函数![]() 在
在![]() 上单调递增;
上单调递增;
④将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,可得函数
个单位长度,可得函数![]() 的图象;
的图象;
⑤![]() 的对称轴方程为
的对称轴方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1,x2,且0<x1<1,x2>1,则 ![]() 的取值范围是( )
的取值范围是( )
A.(-2,- ![]() )
)
B.(-1,- ![]() )
)
C.(-2, ![]() )
)
D.(-1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(![]() sinx+cosx)-
sinx+cosx)-![]() ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)设![]() >0,若函数g(x)=f(x+
>0,若函数g(x)=f(x+![]() )为奇函数,求
)为奇函数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
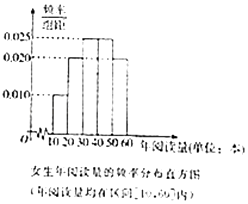
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系中,曲线C1的参数方程为 ![]() (φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(Ⅰ)求曲线C1的极坐标方程与曲线C2的直角坐标方程;
(Ⅱ)若直线θ= ![]() (ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
(ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com