【题目】已知
是两个不重合的平面,下列选项中,一定能得出平面
与平面
平行的是( )
A.平面内有一条直线与平面平行
B.平面内有两条直线与平面平行
C.平面内有一条直线与平面内的一条直线平行
D.平面与平面不相交
【答案】D
【解析】
运用面面平行的判定定理和面面的位置关系等知识对四个选项进行判定.
对于
,由面面平行的判定定理:在一个平面内有两条相交直线与另一个平面平行,则这两个平面平行,所以平面
内有一条直线与平面
平行不能得出平面与平面平行,同时两个平面可能相交,故排除.
对于
,由面面平行的判定定理:在一个平面内有两条相交直线与另一个平面平行,则这两个平面平行, 选项中平面内有两条直线与平面平行,不是两条相交直线,而两条直线有可能是平行线,这样两个面相交时也存在这种情况,所以选项不正确,故排除.
对于
,由面面平行的判定定理:在一个平面内有两条相交直线与另一个平面平行,则这两个平面平行,选项中只有一条直线,故错误,同时当这两个面相交时也可能存在一条线与另一个平面内的一条线平行,故排除.
对于
,平面与平面不相交可以得出平面与平面平行,因为两个平面(不重合)的位置关系只有相交与平行两种,又因为两个平面不相交,所以这两个平面必定平行,所以选项正确.
故选:
三点一测快乐周计划系列答案科目：高中数学 来源： 题型：
【题目】已知函数
，函数
的图象在
处的切线与直线
平行.
（Ⅰ）求实数
的值；
（Ⅱ）若函数
存在单调递减区间，求实数
的取值范围；
（Ⅲ）设
(
)是函数的两个极值点，若
，试求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形
所在的半平面和直角梯形
所在的半平面成
的二面角，
，
，
，
，
，
.
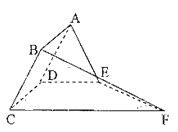
（Ⅰ）求证：平面
平面
；
（Ⅱ）试问在线段
上是否存在一点
，使锐二面角
的余弦值为
.若存在，请求出
的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】图1是由矩形
和菱形
组成的一个平面图形，其中
， 
，将其沿
折起使得
与
重合，连结
，如图2.
（1）证明图2中的
四点共面，且平面
平面
；
（2）求图2中的四边形
的面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图（1）在等腰直角三角形
中，
，将
沿中位线
翻折得到如图（2）所示的空间图形，使二面角
的大小为
.
（1）求证：平面
平面；
（2）若
，求直线
与平面所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，设O为坐标原点，点P的坐标为
记
.
（1）求随机变量
的最大值，并求事件“取得最大值”的概率；
（2）求随机变量的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的有（ ）
①在回归分析中，可以借助散点图判断两个变量是否呈线性相关关系．
②在回归分析中，可以通过残差图发现原始数据中的可疑数据，残差平方和越小，模型的拟合效果越好．
③在回归分析模型中，相关系数的绝对值越大，说明模型的拟合效果越好．
④在回归直线方程
中，当解释变量
每增加1个单位时，预报变量
增加0.1个单位．
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，且过点
.
（1）求椭圆C的标准方程；
（2）点P是椭圆上异于短轴端点A，B的任意一点，过点P作
轴于Q，线段PQ的中点为M.直线AM与直线
交于点N，D为线段BN的中点，设O为坐标原点，试判断以OD为直径的圆与点M的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
