
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),|
=(cosβ,sinβ),| ![]() ﹣
﹣ ![]() |=
|= ![]()
![]() .
.
(1)求cos(α﹣β)的值;
(2)若﹣ ![]() <β<0<α<
<β<0<α< ![]() ,且sinβ=﹣
,且sinβ=﹣ ![]() ,求sinα的值.
,求sinα的值.
【答案】
(1)解:∵ ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),∴|
=(cosβ,sinβ),∴| ![]() |=|
|=| ![]() |=1,
|=1,
∴| ![]() ﹣
﹣ ![]() |2=
|2= ![]() =1+1﹣2(cosαcosβ+sinαsinβ)=2﹣2cos(α﹣β),
=1+1﹣2(cosαcosβ+sinαsinβ)=2﹣2cos(α﹣β),
又∵| ![]() ﹣
﹣ ![]() |=
|= ![]()
![]() ,
,
∴| ![]() ﹣
﹣ ![]() |2=2﹣2cos(α﹣β)=
|2=2﹣2cos(α﹣β)= ![]() ,
,
∴cos(α﹣β)= ![]() ;
;
(2)解:∵﹣ ![]() <β<0<α<
<β<0<α< ![]() ,∴0<α﹣β<π,
,∴0<α﹣β<π,
由cos(α﹣β)= ![]() 可得sin(α﹣β)=
可得sin(α﹣β)= ![]() ,由sinβ=﹣
,由sinβ=﹣ ![]() 可得cosβ=
可得cosβ= ![]() ,
,
∴sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ
= ![]() =
= ![]()
【解析】(1)由模长公式和三角函数公式可得| ![]() ﹣
﹣ ![]() |2=2﹣2co(α﹣β)=
|2=2﹣2co(α﹣β)= ![]() ,变形可得;(2)结合角的范围分别可得sin(α﹣β)=
,变形可得;(2)结合角的范围分别可得sin(α﹣β)= ![]() 和cosβ=
和cosβ= ![]() ,而sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ,代入化简可得.
,而sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ,代入化简可得.
【考点精析】关于本题考查的两角和与差的余弦公式,需要了解两角和与差的余弦公式:![]() 才能得出正确答案.
才能得出正确答案.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点. 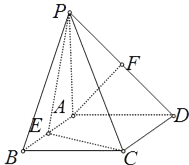
(1)求证:AF∥平面PCE;
(2)求三棱锥C﹣BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:

其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间![]() (单位:小时)与年龄
(单位:小时)与年龄![]() (单位:岁),并制作了对照表(如下表所示)
(单位:岁),并制作了对照表(如下表所示)
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为55岁观众周均学习成语知识时间.
,并预测年龄为55岁观众周均学习成语知识时间.
参考公式: 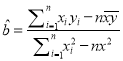 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 内,过
内,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,且点
相交于A,B两点,且点![]() 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.
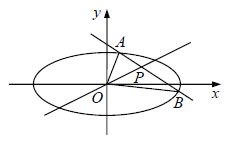
(Ⅰ)是否存在实数t,使直线![]() 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出![]() 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;
(Ⅱ)求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x ,
(1)判断函数的奇偶性;
(2)用函数单调性定义证明:f(x)在(0,+∞)上为单调增函数;
(3)若f(x)=52﹣x+3,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com