Question

设定义域为的函数（为实数）。
（1）若是奇函数，求的值；  
（2）当是奇函数时，证明对任何实数都有成立.

Answer 1

（1），（2）证明过程详见解析.

解析试题分析：本题考查函数的奇偶性和函数最值.考查学生的计算能力和综合分析问题和解决问题的能力.第一问，利用函数的奇函数的性质，列出表达式，化简整理得出关于的恒等式，得出和的值；第二问，证明恒成立问题，经过分析题意，只需证明，所以只需求出和，是通过配方法求出的，是通过分离常数法求出的.
试题解析：(1)(法一)因为是奇函数，所以，
即，∴，∴，
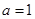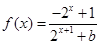∵，∴，∴.(6分)
(法二)因为是奇函数，所以，即对任意实数成立．化简整理得，这是关于的恒等式，所以，所以 (舍)或.
所以.(6分)
(2) ，因为，所以，，
从而；
而对任何实数成立，
所以对任何实数、都有成立．(12分)
考点：1.函数的奇偶性；2.配方法求函数最值；3.分离常数法求函数最值；4.恒成立问题.