
【题目】在三棱柱![]() 中,
中,![]() 与
与![]() 均为等边三角形,
均为等边三角形,![]()
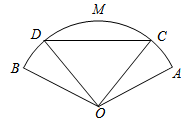
![]() ,O为BC的中点.
,O为BC的中点.
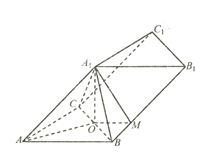
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)在棱![]() 上确定一点M,使得二面角
上确定一点M,使得二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)见解析(2)![]()
【解析】
(1)要证明平面![]() 平面ABC,只需证明
平面ABC,只需证明![]() 平面ABC即可.因为
平面ABC即可.因为![]() 为等边三角形,所以
为等边三角形,所以![]() 再根据勾股定理证明
再根据勾股定理证明![]() ,即可证出
,即可证出![]() 平面ABC;
平面ABC;
(2)以OA,OB,![]() 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系O-xyz,根据向量共线定理用参数
所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系O-xyz,根据向量共线定理用参数![]() 表示出点
表示出点![]() 的坐标,分别求出平面
的坐标,分别求出平面![]() 和平面
和平面![]() 的法向量,由二面角的向量公式列式,即可求出参数
的法向量,由二面角的向量公式列式,即可求出参数![]() ,确定
,确定![]() 的位置.
的位置.
(1)因为![]() 与
与![]() 均为等边三角形,
均为等边三角形,![]() ,O为BC的中点,
,O为BC的中点,
所以![]()
![]() .
.
在![]() 中,
中,![]()
![]() ,
,
从而有![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 平面ABC,
平面ABC,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面ABC.
平面ABC.
(2)以OA,OB,![]() 所在直线分别为x轴,y轴,z轴
所在直线分别为x轴,y轴,z轴
建立如图所示的空间直角坐标系O-xyz,
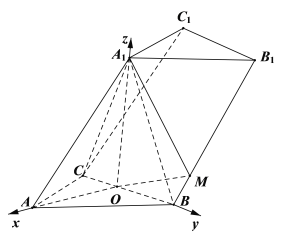
则![]()
![]()
![]()
![]() ,
,
![]() ,由(1)可知,
,由(1)可知,![]() 平面
平面![]() ,
,
![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设![]() ,其中
,其中![]() .
.
所以![]()
![]()
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则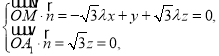
取![]() ,则
,则![]() ,
,
所以![]()
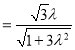
![]() ,
,
解得![]() .
.
即存在一点M,且![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
品牌 | 甲 | 乙 | |||
首次出现故 障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
每辆利润 (万元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个数列的各项是1和2,首项是1,且在第![]() 个1和第
个1和第![]() 个1之间有
个1之间有![]() 个2,即1,2,1,2,2,1,2,2,2,2,1,2,2,2,2,2,2,2,2,1…,则此数列的前2017项的和
个2,即1,2,1,2,2,1,2,2,2,2,1,2,2,2,2,2,2,2,2,1…,则此数列的前2017项的和![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面![]() 平面
平面![]() .现有以下四个结论:
.现有以下四个结论:

①AD∥平面SBC;
②![]() ;
;
③若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积;
④![]() 与平面SCD所成的角为45°.
与平面SCD所成的角为45°.
其中正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为20米,圆心角![]() 的扇形展示台,展示台分成了四个区域:三角形
的扇形展示台,展示台分成了四个区域:三角形![]() ,弓形
,弓形![]() ,扇形
,扇形![]() 和扇形
和扇形![]() (其中
(其中![]() ).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米
).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米![]() ,紫龙卧雪30元/米
,紫龙卧雪30元/米![]() ,朱砂红霜40元/米
,朱砂红霜40元/米![]() .
.
(1)设![]() ,试建立日效益总量
,试建立日效益总量![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试探求![]() 为何值时,日效益总量达到最大值.
为何值时,日效益总量达到最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02.03,…50进行编号,然后从随机数表第9行第11列的数开始向右读,则选出的第6个个体是( )(注:表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.00B.13C.42D.44
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设![]() 为不同的两点,直线
为不同的两点,直线![]() 的方程为
的方程为![]() ,设
,设![]() ,其中
,其中![]() 均为实数.下列四个说法中:
均为实数.下列四个说法中:
①存在实数![]() ,使点
,使点![]() 在直线
在直线![]() 上;
上;
②若![]() ,则过
,则过![]() 两点的直线与直线
两点的直线与直线![]() 重合;
重合;
③若![]() ,则直线
,则直线![]() 经过线段
经过线段![]() 的中点;
的中点;
④若![]() ,则点
,则点![]() 在直线
在直线![]() 的同侧,且直线
的同侧,且直线![]() 与线段
与线段![]() 的延长线相交.
的延长线相交.
所有结论正确的说法的序号是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.35B.0.25C.0.20D.0.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com