分析:(1)A1B1上存在一点D1,满足D1为A1B1的中点,使得C1D1平行于平面ABC.根据线面平行的判定可以证明.
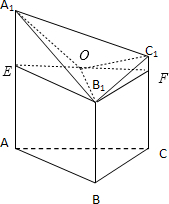
(2)过B1点作AA1,CC1的垂线,垂足为E,F,连接EF,取EF的中点O,则△OC1A1为△C1A1,B1的射影,分别求出面积,利用公式可求;
(3)多面体的体积为VABC-A1B1C1+VB1-EFC1A1,分别计算,即可求得.
解答: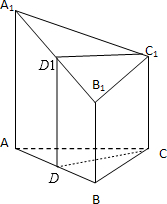
解:(1)A
1B
1上存在一点D
1,满足D
1为A
1B
1的中点,使得C
1D
1平行于平面ABC.
D
1为A
1B
1的中点,取AB 的中点D,连接DD
1,C
1D
1,
∵多面体ABC-A
1B
1C
1是由直棱柱被平面A
1B
1C
1而成
∴AA
1∥BB
1∥CC
1,
∵AA
1=4,BB
1=2,D
1为A
1B
1的中点,取AB 的中点D,
∴DD
1∥CC
1,且DD
1=CC
1=3
∴四边形CDD
1C
1为平行四边形
∴D
1C
1∥DC
∵D
1C
1?平面ABC,DC?平面ABC
∴C
1D
1∥平面ABC.
(2)过B
1点作AA
1,CC
1的垂线,垂足为E,F,连接EF,取EF的中点O,则B
1O⊥平面C
1A
1B
1,
∵AB与BC垂直,AB=BC=1
∴EB
1=FB
1=1,EF=
∵OB
1=
,
∵AA
1=4,BB
1=2,CC
1=3
∴C
1F=1
∴A
1B
1=
,B
1C
1=
,A
1C
1=
∴△A
1B
1C
1为直角三角形,
∴B
1C
1⊥A
1C
1,
∵B
1O⊥平面C
1A
1B
1,
∴OC
1⊥平面C
1A
1B
1,
∴∠OC
1B
1为二面角B
1-A
1C
1-A的平面角
∵sin∠OC
1B
1=
=
=
∴∠OC
1B
1=30°
∴二面角B
1-A
1C
1-A的大小为30°
(3)四边形EFC
1A
1的面积为
×=
,B
1O=
多面体的体积为
VABC-A1B1C1+VB1-EFC1A1=
×1×1×2+
××=
点评:本题重点考查线面平行,面面角,考查多面体的体积,解题的关键是用好线面平行的判定,确定射影面积,及分割法求多面体的体积,综合性强,难度大.

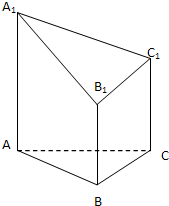 如图所示,多面体ABC-A1B1C1是由直棱柱被平面A1B1C1而成.其中AA1=4,BB1=2,CC1=3,AB与BC垂直,AB=BC=1
如图所示,多面体ABC-A1B1C1是由直棱柱被平面A1B1C1而成.其中AA1=4,BB1=2,CC1=3,AB与BC垂直,AB=BC=1 解:(1)A1B1上存在一点D1,满足D1为A1B1的中点,使得C1D1平行于平面ABC.
解:(1)A1B1上存在一点D1,满足D1为A1B1的中点,使得C1D1平行于平面ABC.


 阅读快车系列答案
阅读快车系列答案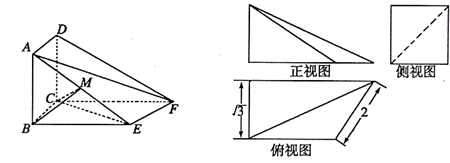
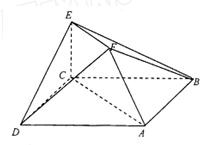 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB= 在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
 如图所示,多面体EF-ABCD中,ABCD是直角梯形,AB⊥AD,AB∥DC,∠ABC=60°,FC⊥平面ABCD,正△ADE⊥平面ABCD,FC=2DC=6,AD=2
如图所示,多面体EF-ABCD中,ABCD是直角梯形,AB⊥AD,AB∥DC,∠ABC=60°,FC⊥平面ABCD,正△ADE⊥平面ABCD,FC=2DC=6,AD=2