
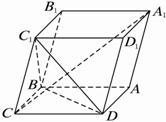
解析:设![]() =a,
=a,![]() =b,
=b,![]() =c,
=c,
由已知|a|=|b|,
![]() ·
·![]() =(a+ b+ c)(a-b)=|a|2-|b|2+a·c-b·c=|a||c|·cos60°-|b||c|·cos60°=0,
=(a+ b+ c)(a-b)=|a|2-|b|2+a·c-b·c=|a||c|·cos60°-|b||c|·cos60°=0,
∴CA1⊥BD.
因而A1C⊥平面C1BD的充要条件是CA1⊥C1D.
由![]() ⊥
⊥![]()
![]()
![]() ·
·![]() =(a+ b+ c)·(a-c)=0
=(a+ b+ c)·(a-c)=0![]() |a|2+a·b-b·c-|c|2=0?|a|2+|a|·|b|·cos60°-|b|·|c|·cos60°-|c|2=0
|a|2+a·b-b·c-|c|2=0?|a|2+|a|·|b|·cos60°-|b|·|c|·cos60°-|c|2=0![]() (3|a|+2|c|)·(|c|-|a|)=0.
(3|a|+2|c|)·(|c|-|a|)=0.
∵|a|>0,|c|>0,∴|a|=|c|.
∴当![]() =1时,A1C⊥平面C1BD.
=1时,A1C⊥平面C1BD.
温馨提示:这是条件开放性问题,从结论出发,利用向量垂直的条件由线线垂直推出线面垂直.本题通过利用向量的几何运算法则及向量的数量积运算大大降低了探索难度.


科目:高中数学 来源: 题型:
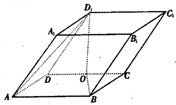 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
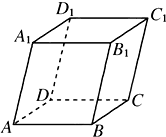 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,查看答案和解析>>
科目:高中数学 来源:2013届湖北省武汉市高二下期末理科数学试卷(解析版) 题型:解答题
题满分12分)
.如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
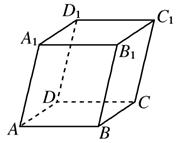
(1)当AA1=3,AB=2,AD=2,求AC1的长;
(2)当底面ABCD是菱形时,求证: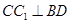
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市萧山区三校联考高二(上)期中数学试卷(理科)(解析版) 题型:填空题
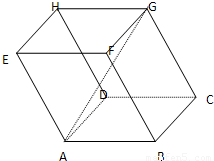
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com