
【题目】判断下列命题的真假.
(1)过不在平面内的一点,有且只有一个平面与这个平面平行;
(2)过不在平面内的一条直线,有且只有一个平面与这个平面平行;
(3)给定两个平行平面中一个平面内的一条直线,则在另一个平面内有且只有一条直线与这条直线平行.
【答案】(1)真命题;(2)假命题;(3)假命题.
【解析】
根据面面平行的判定定理知过平面外可作出一个平面平行已知平面,用反证法证明只有一个平面满足,可判断(1)的真假;根据直线与平面的位置关系,判断(2)的真假;根据面面平行的性质定理,可判断(3)的真假.
(1)设平面![]() ,点
,点![]() ,在平面
,在平面![]() 作两条相交的直线
作两条相交的直线![]() ,
,
过点![]() 作两直线
作两直线![]() ,使得
,使得![]() ,则
,则![]() 确定平面
确定平面![]() ,
,
![]() ,
,![]() ,
,![]() ,同理
,同理![]() ,
,![]() ,所以
,所以![]() .
.
假设还存在一个平面![]() ,
,
则有![]() ,与
,与![]() 存在公共点
存在公共点![]() 矛盾,故假设不成立,
矛盾,故假设不成立,
即满足条件的平面有且只有一个,所以(1)为真命题;
(2)若直线与平面相交,则过这条直线不存在平面与这个平面平行,所以(2)是假命题;
(3)给定两个平行平面中一个平面内的一条直线,根据面面平行性质定理和平行线的传递性,则在另一个平面内有无数条直线与这条直线平行,所以(3)是假命题.
综上:(1)真命题;(2)假命题;(3)假命题.


科目:高中数学 来源: 题型:
【题目】某校社团活动开展有声有色,极大地推动了学生的全面发展,深受学生欢迎,每届高一新生都踊跃报名加入.现已知高一某班有6名男同学和4名女同学参加心理社,在这10名同学中,4名同学初中毕业于同一所学校,其余6名同学初中毕业于其他6所不同的学校.现从这10名同学中随机选取4名同学代表社团参加校际交流(每名同学被选到的可能性相同).
(Ⅰ)求选出的4名同学初中毕业于不同学校的概率;
(Ⅱ)设![]() 为选出的4名同学中女同学的人数,求随机变量
为选出的4名同学中女同学的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的最值.
的距离的最值.
【答案】(1)![]() ,
, ![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]()
【解析】试题分析:(1)根据参数方程和极坐标化普通方程化法即易得结论![]() 的普通方程为
的普通方程为![]() ;直线
;直线![]() 的普通方程为
的普通方程为![]() .(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设
.(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设![]() ,
, ![]()
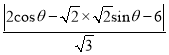
![]()
 .即可得出最值
.即可得出最值
解析:(1)根据题意,由 ,得
,得![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的普通方程为
的普通方程为![]() ;
;
由![]() 及
及![]() ,
, ![]() 得
得![]() ,
,
故直线![]() 的普通方程为
的普通方程为![]() .
.
(2)由于![]() 为曲线
为曲线![]() 上任意一点,设
上任意一点,设![]() ,
,
由点到直线的距离公式得,点![]() 到直线
到直线![]() 的距离为
的距离为
![]()

![]()
 .
.
∵![]()
![]() ,
,
∴
 ,即
,即![]()
![]() ,
,
故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:首先要熟悉参数方程和极坐标方程化普通方程的方法,第一问基本属于送分题所以务必抓住,对于第二问可以总结为一类题型,借助参数方程设点的方便转化为三角函数最值问题求解
【题型】解答题
【结束】
23
【题目】已知函数![]() ,
,![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)若函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的上方,求
图象的上方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(Ⅰ)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(Ⅱ)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟用10万元投资甲、乙两种商品.已知各投入![]() 万元,甲、乙两种商品分别可获得
万元,甲、乙两种商品分别可获得![]() 万元的利润,利润曲线
万元的利润,利润曲线![]() ,
,![]() ,如图所示.
,如图所示.

(1)求函数![]() 的解析式;
的解析式;
(2)应怎样分配投资资金,才能使投资获得的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的
年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的![]() 抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后
抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后![]() 分钟,瓶内液面与进气管的距离为
分钟,瓶内液面与进气管的距离为![]() 厘米,已知当
厘米,已知当![]() 时,
时,![]() .如果瓶内的药液恰好
.如果瓶内的药液恰好![]() 分钟滴完.则函数
分钟滴完.则函数![]() 的图像为( )
的图像为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com