
在斜三棱柱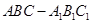 中,平面
中,平面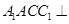 平面ABC,
平面ABC,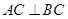 ,
,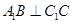 ,
,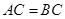 .
.
(1)求证: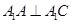 ;
;
(2)若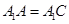 ,求二面角
,求二面角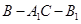 的余弦值.
的余弦值.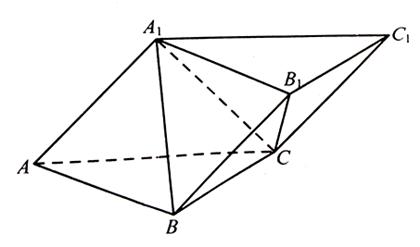
(1)证明过程详见解析;(2)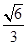 .
.
解析试题分析:本题主要考查线线垂直、线面垂直、面面垂直、线线平行、二面角的余弦等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,利用面面垂直的性质得BC⊥平面A1ACC1,则利用线面垂直的性质得A1A⊥BC,由A1B⊥C1C,利用平行线A1A∥C1C,则A1A⊥A1B,利用线面垂直的判定得A1A⊥平面A1BC,则利用线面垂直的性质得A1A⊥A1C;第二问,建立空间直角坐标系,得到面上的点的坐标,计算出向量坐标,求出平面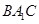 和平面
和平面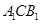 的法向量,利用夹角公式计算出二面角的余弦值.
的法向量,利用夹角公式计算出二面角的余弦值.
(1)因为平面A1ACC1⊥平面ABC,AC⊥BC,所以BC⊥平面A1ACC1,
所以A1A⊥BC.
因为A1B⊥C1C,A1A∥C1C,所以A1A⊥A1B,
所以A1A⊥平面A1BC,所以A1A⊥A1C. 5分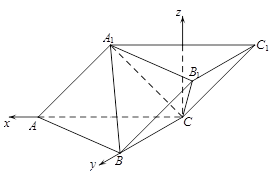
(2)建立如图所示的坐标系C-xyz.
设AC=BC=2,因为A1A=A1C,
则A(2,0,0),B(0,2,0),A1(1,0,1),C(0,0,0).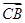 =(0,2,0),
=(0,2,0), =(1,0,1),
=(1,0,1), =(-2,2,0).
=(-2,2,0).
设n1=(a,b,c)为面BA1C的一个法向量,则n1·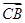 =n1·
=n1· =0,
=0,
则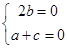 ,取n1=(1,0,-1).
,取n1=(1,0,-1).
同理,面A1CB1的一个法向量为n2=(1,1,-1). 9分
所以cosán1,n2ñ=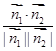 =
=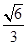 ,
,
故二面角B-A1C-B1的余弦值为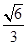 . 12分
. 12分
考点:线线垂直、线面垂直、面面垂直、线线平行、二面角的余弦.


科目:高中数学 来源: 题型:解答题
如图,四棱柱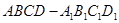 中,
中,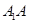
 底面
底面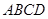 .四边形
.四边形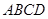 为梯形,
为梯形, ,且
,且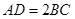 .过
.过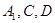 三点的平面记为
三点的平面记为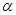 ,
,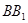 与
与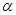 的交点为
的交点为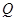 .
.
(1)证明: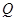 为
为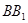 的中点;
的中点;
(2)求此四棱柱被平面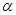 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;
(3)若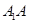
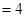 ,
,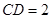 ,梯形
,梯形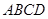 的面积为6,求平面
的面积为6,求平面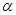 与底面
与底面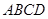 所成二面角大小.
所成二面角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在边长为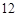 的正方形
的正方形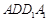 中,点
中,点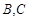 在线段
在线段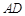 上,且
上,且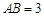 ,
,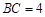 ,作
,作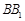 //
//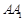 ,分别交
,分别交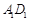 ,
,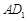 于点
于点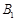 ,
,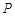 ,作
,作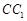 //
//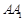 ,分别交
,分别交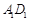 ,
,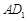 于点
于点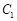 ,
,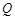 ,将该正方形沿
,将该正方形沿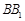 ,
,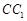 折叠,使得
折叠,使得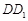 与
与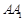 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱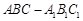 .
.
(1)求证: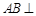 平面
平面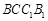 ;
;
(2)若点E为四边形BCQP内一动点,且二面角E-AP-Q的余弦值为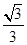 ,求|BE|的最小值.
,求|BE|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
(1)证明:BD⊥AA1;
(2)求锐二面角D-A1A-C的平面角的余弦值;
(3)在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且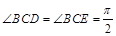 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.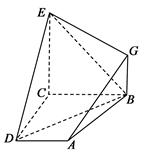
(1)求证:AG 平面BDE;
平面BDE;
(2)求:二面角G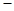 DE
DE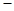 B的余弦值.
B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com