
【题目】已知圆![]() ,直线
,直线![]() 被圆所截得的弦的中点为
被圆所截得的弦的中点为![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交, 求
相交, 求![]() 的取值范围;
的取值范围;
(3)是否存在常数![]() ,使得直线
,使得直线![]() 被圆
被圆![]() 所截得的弦中点落在直线
所截得的弦中点落在直线![]() 上?若存在, 求出
上?若存在, 求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)设直线![]() 的斜率为则
的斜率为则![]() ,由题意可得圆心
,由题意可得圆心![]() ,又弦的中点为
,又弦的中点为![]() ,可求得
,可求得![]() ,由
,由![]() 可求
可求![]() ,从而可求直线
,从而可求直线![]() 的方程;(2)若直线
的方程;(2)若直线![]() :
:![]() 与圆
与圆![]() 相交,圆心到直线
相交,圆心到直线![]() 的距离小于半径,从而可求得
的距离小于半径,从而可求得![]() 的取值范围;(3)设直线
的取值范围;(3)设直线![]() 被圆
被圆![]() 解得的弦的中点为
解得的弦的中点为![]() ,由直线
,由直线![]() 与
与![]() 垂直,可得
垂直,可得![]() ,与
,与![]() 联立可求得
联立可求得![]() ,代入直线
,代入直线![]() 的方程,求得
的方程,求得![]() ,验证即可.
,验证即可.
试题解析:(1)圆![]() 方程化为标准方程:
方程化为标准方程:![]() ,则其圆心
,则其圆心![]() ,半径
,半径![]() ,若设直线
,若设直线![]() 的斜率为
的斜率为![]() ,则
,则 ,
,![]() 直线
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(2)![]() 圆的半径
圆的半径![]() ,
,![]() 要直线
要直线![]() 与圆
与圆![]() 相交, 则须有
相交, 则须有![]() ,于是
,于是![]() 的取值范围是
的取值范围是![]() .
.
(3)设直线![]() 被圆
被圆![]() 截得的弦的中点为
截得的弦的中点为![]() ,则直线
,则直线![]() 与
与![]() 垂直, 于是有
垂直, 于是有![]() ,整理可得
,整理可得![]() ,又
,又![]() 点
点![]() 在直线
在直线![]() 上,
上, ![]() ,
,![]() 由
由 ,解得
,解得 ,代入直线
,代入直线![]() 的方程, 得
的方程, 得![]() ,于是
,于是![]() ,故存在满足条件的常数
,故存在满足条件的常数![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】已知某中学联盟举行了一次“盟校质量调研考试”活动.为了解本次考试学生的某学科成绩情况,从中抽取部分学生的分数(满分为100分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本(样本容量为n)进行统计.按照
之内)作为样本(样本容量为n)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(茎叶图中仅列出了得分在![]() ,
,![]() 的数据).
的数据).
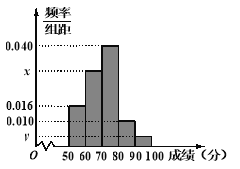
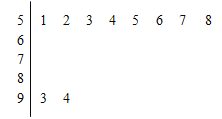
(Ⅰ)求样本容量n和频率分布直方图中的x、y的值;
(Ⅱ)在选取的样本中,从成绩在80分以上(含80分)的学生中随机抽取2名学生参加“省级学科基础知识竞赛”,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区准备将一块闲置的直角三角形(其中![]() )土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道
)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ),现考虑方便和绿地最大化原则,要求
),现考虑方便和绿地最大化原则,要求![]() 点与
点与![]() 点不重合,
点不重合,![]() 点落在边
点落在边![]() 上,设
上,设![]() .
.
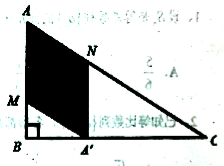
(1)若![]() ,绿地“最美”,求最美绿地的面积;
,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求![]() 最短,求此时公共绿地走道
最短,求此时公共绿地走道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一![]() 名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分
名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分![]() 分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
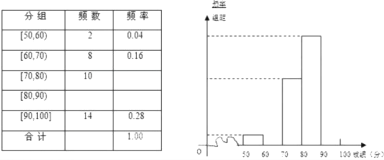
(1)填写答题卡频率分布表中的空格, 补全频率分布直方图, 并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级的平均数及中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将甲、乙、丙、丁四名同学按一定顺序排成一行,要求自左向右,且甲不排在第一,乙不排在第二,丙不排在第三,丁不排在第四,比如:“乙甲丁丙”是满足要求的一种排法,试写出他们四个人所有不同的排法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要产生[-3,3]上的均匀随机数y,现有[0,1]上的均匀随机数x,则y可取为( )
A. -3x B. 3x
C. 6x-3 D. -6x-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com