
【题目】若数列![]() 中存在三项,按一定次序排列构成等比数列,则称
中存在三项,按一定次序排列构成等比数列,则称![]() 为“等比源数列”。
为“等比源数列”。
(1)在无穷数列![]() 中,
中,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的结论下,试判断数列![]() 是否为“等比源数列”,并证明你的结论;
是否为“等比源数列”,并证明你的结论;
(3)已知无穷数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 为“等比源数列”.
为“等比源数列”.
【答案】(1)![]() ;(2)不是,证明见解析;(3)证明见解析.
;(2)不是,证明见解析;(3)证明见解析.
【解析】
(1)由![]() ,可得出
,可得出![]() ,则数列
,则数列![]() 为等比数列,然后利用等比数列的通项公式可间接求出
为等比数列,然后利用等比数列的通项公式可间接求出![]() ;
;
(2)假设数列![]() 为“等比源数列”,则此数列中存在三项
为“等比源数列”,则此数列中存在三项![]() 成等比数列,可得出
成等比数列,可得出![]() ,展开后得出
,展开后得出![]() ,然后利用数的奇偶性即可得出结论;
,然后利用数的奇偶性即可得出结论;
(3)设等差数列![]() 的公差为
的公差为![]() ,假设存在三项使得
,假设存在三项使得![]() ,展开得出
,展开得出![]() ,从而可得知,当
,从而可得知,当![]() ,
,![]() 时,原命题成立.
时,原命题成立.
(1)![]() ,得
,得![]() ,即
,即![]() ,且
,且![]() .
.
所以,数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,则
为公比的等比数列,则![]() ,
,
因此,![]() ;
;
(2)数列![]() 不是“等比源数列”,下面用反证法来证明.
不是“等比源数列”,下面用反证法来证明.
假设数列![]() 是“等比源数列”,则存在三项
是“等比源数列”,则存在三项![]() 、
、![]() 、
、![]() ,设
,设![]() .
.
由于数列![]() 为单调递增的正项数列,则
为单调递增的正项数列,则![]() ,所以
,所以![]() .
.
得![]() ,化简得
,化简得![]() ,
,
等式两边同时除以![]() 得
得![]() ,
,
![]() ,且
,且![]() 、
、![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() 为偶数,
为偶数,![]() 为奇数,等式
为奇数,等式![]() 不成立.
不成立.
因此,数列![]() 中不存在任何三项,按一定的顺序排列构成“等比源数列”;
中不存在任何三项,按一定的顺序排列构成“等比源数列”;
(3)不妨设等差数列![]() 的公差
的公差![]() .
.
当![]() 时,等差数列
时,等差数列![]() 为非零常数列,此时,数列
为非零常数列,此时,数列![]() 为“等比源数列”;
为“等比源数列”;
当![]() 时,
时,![]() ,则
,则![]() 且
且![]() ,
,![]() 数列
数列![]() 中必有一项
中必有一项![]() ,
,
为了使得数列![]() 为“等比源数列”,只需数列
为“等比源数列”,只需数列![]() 中存在第
中存在第![]() 项、第
项、第![]() 项使得
项使得![]() ,
,
且有![]() ,即
,即![]() ,
,
![]() ,
,
当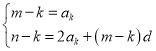 时,即当
时,即当![]() ,
,![]() 时,
时,
等式![]() 成立,
成立,
所以,数列![]() 中存在
中存在![]() 、
、![]() 、
、![]() 成等比数列,因此,等差数列
成等比数列,因此,等差数列![]() 是“等比源数列”.
是“等比源数列”.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知椭圆![]() ,设
,设![]() 是椭圆
是椭圆![]() 上任一点,从原点
上任一点,从原点![]() 向圆
向圆![]() 作两条切线,切点分别为
作两条切线,切点分别为![]() .
.
(1)若直线![]() 互相垂直,且点
互相垂直,且点![]() 在第一象限内,求点
在第一象限内,求点![]() 的坐标;
的坐标;
(2)若直线![]() 的斜率都存在,并记为
的斜率都存在,并记为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 、
、![]() 满足:
满足:![]() ,
,![]() ,记
,记![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)定义![]() ,证明:若存在
,证明:若存在![]() ,使得
,使得![]() 、
、![]() 为整数,且
为整数,且![]() 有两个整数零点,则必有无穷多个
有两个整数零点,则必有无穷多个![]() 有两个整数零点.
有两个整数零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com