
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,试讨论函数
时,试讨论函数![]() 的单调性;
的单调性;
(Ⅲ)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]() (
(![]() ),证明:
),证明:![]() .
.
【答案】(I)![]() ;(II)当
;(II)当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() 在
在![]() 上单调递增;(III)证明见解析.
上单调递增;(III)证明见解析.
【解析】
试题分析:(I)当![]() 时,
时,![]() ,根据
,根据![]() ,
,![]() ,求得切线方程为
,求得切线方程为![]() ;(II)定义域为
;(II)定义域为![]() ,求导得
,求导得![]() ,由
,由![]() 得,
得,![]() ,
,![]() ,对
,对![]() 分成
分成![]() 类,结合函数图像进行分类讨论
类,结合函数图像进行分类讨论![]() 的单调区间;(III)先用分析法分析,要证
的单调区间;(III)先用分析法分析,要证![]() ,即证
,即证![]() ,因
,因![]() ,即证
,即证![]() ,令
,令![]() (
(![]() ),即证
),即证![]() (
(![]() ),令
),令![]() 利用导数可证明上述不等式成立.
利用导数可证明上述不等式成立.
试题解析:
(Ⅰ)依题意得![]() ,则
,则![]() ,
,![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)∵函数![]() 的定义域为
的定义域为![]() ,且
,且
![]()
![]() ,
,
当![]() 时,由
时,由![]() 得,
得,![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,由
,由![]() 得,
得,![]() ,或
,或![]() ;由
;由![]() 得,
得,![]() ,所以
,所以![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减……6分
上单调递减……6分
③ 当![]() 时,
时,![]() ,由
,由![]() 得,
得,![]() ,或
,或![]() ;由
;由![]() 得,
得,![]() ,
,
所以![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
③当![]() 时,
时,![]() ,在
,在![]() 上,
上,![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
综上,当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
(Ⅲ)依题意得![]() ,
,
要证![]() ,即证
,即证![]() ,
,
因![]() ,即证
,即证![]() ,
,
令![]() (
(![]() ),即证
),即证![]() (
(![]() ),
),
令![]() (
(![]() )则
)则![]()
![]() ,
,
∴![]() 在(1,+
在(1,+![]() )上单调递增,
)上单调递增,
∴![]() =0,即
=0,即![]() (
(![]() )①
)①
同理可证:![]() ②
②
综①②得![]() (
(![]() ),即
),即![]()


科目:高中数学 来源: 题型:
【题目】不等式|2x-log2x|<|2x|+|log2x|的解集为( )
A. {x|1<x<2} B. {x|0<x<1} C. {x|x>1} D. {x|x>2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合 A={1,2,3},B={2,3,4},则 A∪B( )
A. {1,2,3,4} B. {1,2,3} C. {2,3,4} D. {1,3,4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 相关关系是一种不确定的关系,回归分析是对相关关系的分析,因此没有实际意义
B. 独立性检验对分类变量关系的研究没有100%的把握,所以独立性检验研究的结果在实际中也没有多大的实际意义
C. 相关关系可以对变量的发展趋势进行预报,这种预报可能是错误的
D. 独立性检验如果得出的结论有99%的可信度就意味着这个结论一定是正确的
查看答案和解析>>
科目:高中数学 来源: 题型:
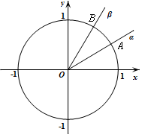
【题目】如图,在平面直角坐标系中,锐角![]() 、
、![]() 的终边分别与单位圆交于
的终边分别与单位圆交于![]() ,
,![]() 两点.
两点.
(1)如果![]() ,
,![]() 点的横坐标为
点的横坐标为![]() ,求
,求![]() 的值;
的值;
(2)若角![]() 的终边与单位圆交于C点,设角
的终边与单位圆交于C点,设角![]() 、
、![]() 、
、![]() 的正弦线分别为
的正弦线分别为![]() ,求证:线段
,求证:线段![]() 能构成一个三角形;
能构成一个三角形;
(3)探究第(2)小题中的三角形的外接圆面积是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有_________种. (用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园为了了解全园310名小班学生的身高情况,从中抽取31名学生进行身高测量、下列说法正确的是( )
A. 总体是310 B. 310名学生中的每一名学生都是个体
C. 样本是31名小班学生 D. 样本容量是31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com