
如下图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.求BD的长.

|
解:在△ ABC中,AB=5,AC=9,∠BCA=30°.由正弦定理,得
∵ AD∥BC,∴∠BAD=180°-∠ABC,于是
同理,在△ ABD中,AB=5,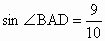 ,∠ADB=45°,解得 ,∠ADB=45°,解得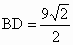 . .
答: BD的长为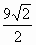 . .
|
|
求解三角形中的几何计算问题时,要首先确定与未知量之间相关联的量,把所要求的问题转化为由已知条件可直接求解的量上来. 由于 AB=5,∠ADB=45°,因此要求BD,可在∠ABD中,由正弦定理求解,关键是确定∠BAD的正弦值,在△ABC中,AB=5,AC=9,∠ACB=30°,因此可用正弦定理求出sin ∠ABC,再依据∠ABC与∠BAD互补确定sin ∠BAD即可. |


科目:高中数学 来源: 题型:
(09年山东苍山期末文)(12分)
如下图所示:在直三棱柱ABC―A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点。

(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com