练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在xOy平面上，将双曲线的一支 及其渐近线和直线、围成的封闭图形记为D，如图中阴影部分，记D绕y轴旋转一周所得的几何体为，过 作的水平截面，计算截面面积，利用祖暅原理得出体积为________

    【答案】.

    【解析】分析：由已知中过（0，y）（0≤y≤4）作Ω的水平截面，计算截面面积，利用祖暅原理得出Ω的体积．

    详解：在xOy平面上，将双曲线的一支 及其渐近线和直线y=0，y=4围成的封闭图形记为D，如图中阴影部分．

    则直线y=a与渐近线交于一点A（，a）点，与双曲线的一支 交于B（，a）点，

    记D绕y轴旋转一周所得的几何体为Ω．

    过（0，y）（0≤y≤4）作Ω的水平截面，

    则截面面积S=，

    利用祖暅原理得Ω的体积相当于底面面积为9π高为4的圆柱的体积，

    ∴Ω的体积V=9π×4=36π，

    故答案为：36π

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    (1)当时,讨论的单调性；

    (2)设，当时,若对任意,存在使,求实数取值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（12分）
    （1）证明：平面PAB⊥平面PAD；
    （2）若PA=PD=AB=DC，∠APD=90°，求二面角A﹣PB﹣C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，平面平面，四边形为正方形，四边形为梯形，且，，．

    （Ⅰ）求证：平面；

    （Ⅱ）求证：平面；

    （Ⅲ）在线段上是否存在点，使得平面？若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BAC=90°．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．

    （Ⅰ）求证：MN∥平面BDE；
    （Ⅱ）求二面角C﹣EM﹣N的正弦值；
    （Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为 ，求线段AH的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现在，很多人都喜欢骑“共享单车”，但也有很多市民并不认可．为了调查人们对这种交通方式的认可度，某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民，得到了一个市民是否认可的样本，具体数据如下列联表：

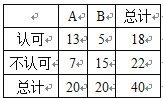
    附：，．

    根据表中的数据，下列说法中，正确的是（ ）

    A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”

    B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”

    C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”

    D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知直线的参数方程为（为参数）.以坐标原点为极点，以坐标原点为极点，轴的非负半轴为极轴，取相同的长度单位建立极坐标系，曲线的极坐标方程为.

    (Ⅰ)求直线的普通方程和曲线的直角坐标方程；

    (Ⅱ)若曲线上的点到直线的最大距离为6，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是菱形，对角线，交于点．

    （Ⅰ）若，求证：平面；

    （Ⅱ）若平面平面，求证：；

    （Ⅲ）在棱上是否存在点（异于点），使得平面？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究机构对高三学生的记忆力和判断力进行统计分析，得下表数据：

    （1）请根据上表提供的数据，用相关系数说明与的线性相关程度；（结果保留小数点后两位，参考数据: ）

    （2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （3）试根据求出的线性回归方程，预测记忆力为9的同学的判断力．

    参考公式：，；相关系数；

    查看答案和解析>>

    同步练习册答案