分析:按题意:直线AO垂直于直线B1O,三角形为AOB1为直角三角形,O点在以|AB1|为直径的球面上;设球面中心点为P,则点P位于线段|AB1|的中点;此时答案变为求球外一点至球面上一点的距离;按题意:存在直角三角形C1B1P,线段|C1P|为斜边(点C1至球心P的距离);此时:存在任意三角形C1PO,其中线段|C1P|为C1点至球心P的距离、线段|PO|为球面半径,线段|C1O|的长度是我们要的答案.
解答:解:∵直线AO(即l)垂直于α,直线B
1O?α,
∴三角形AOB
1为直角三角形,
∴O点在以|AB
1|为直径的球面上;设球面中心点为P,则点P位于线段|AB
1|的中点;
又长方体ABCD-A
1B
1C
1D
1中,|AD|=5,|AB|=6,|AA
1|=8,
∴|AB
1|=10,
|OP|==5,
此时所求变为求球外一点至球面上一点的距离;显然当C
1,P,O三点共线时|C
1O|最大,
∵在直角三角形C
1B
1P,线段|C
1P|为斜边(点C
1至球心P的距离),
∴
|C1P| =5,
∴|C
1O|
max=|C
1P|+|OP|=
5+5.
故答案为:
5+5.
点评:本题考查函数的值域,难点在于转化为球外一点至球面上一点的距离,显然最大时必过球心,是难题.

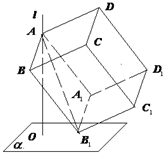 已知直线l⊥平面α,O为垂足,长方体ABCD-A1B1C1D1中,AD=5,AB=6,AA1=8,A∈l,B1∈α,则OC1的最大值为
已知直线l⊥平面α,O为垂足,长方体ABCD-A1B1C1D1中,AD=5,AB=6,AA1=8,A∈l,B1∈α,则OC1的最大值为

 阅读快车系列答案
阅读快车系列答案