
����Ŀ����һ��ͬѧ�ҿ���һ���̲�꣬��Ϊ���о����¶����̲����۱�����Ӱ�죬��һ���������ѡȡ5�죬ͳ�Ƴ����������̲����۱����������
���� | 0 | 4 | 12 | 19 | 27 |
���̲����۱��� | 150 | 132 | 130 | 104 | 94 |
���������̲����۱����������µ����Իع鷽��![]() ��
��![]() ��ȷ��0.1������ij�������Ϊ
��ȷ��0.1������ij�������Ϊ![]() ��Ԥ���������̲�����۱�����
��Ԥ���������̲�����۱�����
���ӱ��е�5������ȡ���죬����ѡȡ������������һ�����̲����۱�������130�ĸ��ʣ�
�ο����ݣ�![]() ��
��![]() .
.
�ο���ʽ��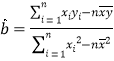 ��
��![]() ��
��
���𰸡���1��![]() ��2.0x+146.8��Ԥ������Ϊ15oC�����̲�����Լ117������2��
��2.0x+146.8��Ԥ������Ϊ15oC�����̲�����Լ117������2��![]() ��
��
��������
��1���ɱ��������ݼ���![]() ��
��![]() ������ع�ϵ������д���ع鷽�̣�
������ع�ϵ������д���ع鷽�̣�
���ûع鷽����ö�Ӧ![]() ��ֵ��
��ֵ��
��2�������оٷ���������¼������ټ�������ĸ���ֵ��
��1���ɱ��������ݿɵã�
![]() =
=![]() ����0+4+12+19+27��=12.4��
����0+4+12+19+27��=12.4��![]() =
=![]() ����150+132+130+104+94��=122��
����150+132+130+104+94��=122��
��![]() =
=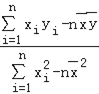 =
=![]() �֩�2.0��
�֩�2.0��
![]() =
=![]()
![]()
![]() =122������2.0����12.4=146.8��
=122������2.0����12.4=146.8��
�����̲����۱����������µ����Իع鷽��Ϊ
![]() =��2.0x+146.8��
=��2.0x+146.8��
��x=15ʱ��![]() =��2.0��15+146.8=116.8��117��
=��2.0��15+146.8=116.8��117��
��Ԥ������Ϊ15oC���������̲�����Լ117����
��2���DZ��еĵ�1�쵽��5��ΪA��B��c��d��e���������۱�������130����A��B��
��ȡ������AB��Ac��Ad��Ae��Bc��Bd��Be��cd��ce��de��10�������
����������һ�����۱�������130��AB��Ac��Ad��Ae��Bc��Be��7�������
����ѡȡ������������һ�����̲����۱�������130�ĸ���ΪP=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() �����䳤�᳤Ϊ__________����
�����䳤�᳤Ϊ__________����![]() Ϊ
Ϊ![]() ���ҽ��㣬
���ҽ��㣬 ![]() Ϊ
Ϊ![]() ���϶��㣬
���϶��㣬 ![]() Ϊ
Ϊ![]() ��λ�ڵ�һ�����ڵĶ��㣬���ı���
��λ�ڵ�һ�����ڵĶ��㣬���ı���![]() ����������ֵΪ__________��
����������ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ������
������![]() ������������
������������![]() Ϊ�������Σ��߳�Ϊ
Ϊ�������Σ��߳�Ϊ![]() ������
������![]() ��ƽ��
��ƽ��![]() �ϵ���ӰΪ
�ϵ���ӰΪ![]() ����
����![]() ����
����![]() .
.
������֤�� ![]() ƽ��
ƽ��![]() ��
��
����������![]() ������ֵ��
������ֵ��
�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ʹ��
ʹ��![]() ��ƽ��
��ƽ��![]() ��������ڣ���
��������ڣ���![]() ��ֵ����������ڣ���˵������.
��ֵ����������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ��ʾ�ij����ͼ��������Ľ���ǣ� �� 
A.e2016��e2015
B.e2017��e2016
C.e2015��1
D.e2016��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() �ĵ�����ΪA��0��-2����C��4��2����B��4��-2����D��0��2����
�ĵ�����ΪA��0��-2����C��4��2����B��4��-2����D��0��2����

��1����Խ���![]() ����ֱ�ߵķ��̣�
����ֱ�ߵķ��̣�
��2�������![]() ���Բ�ķ��̣�
���Բ�ķ��̣�
��3��������![]() Ϊ���Բ��һ�㣬��
Ϊ���Բ��һ�㣬��![]() Ϊ���㣬���߶�PN�е�Ĺ켣��ʲô��������ù켣���̡�
Ϊ���㣬���߶�PN�е�Ĺ켣��ʲô��������ù켣���̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������E��y2=2px��p��0��������x�ύ�ڵ�K������K��Բ��x��5��2+y2=9���������ߣ��е�ΪM��N��|MN|=3 ![]()
��1����������E�ķ��̣�
��2����A��B��������E�Ϸֱ�λ��x��������������㣬�� ![]() ������OΪ����ԭ�㣩��
������OΪ����ԭ�㣩��
����֤��ֱ��AB�ع����㣬������ö���Q�����ꣻ
�ڹ���Q��AB�Ĵ����������߽���G��D���㣬���ı���AGBD�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() ��a��b��0����ͼ��������C��
��a��b��0����ͼ��������C�� 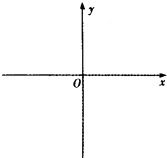
��1������ͼ������ϵ�зֱ���������C��ʾ��ͼ�����ֱ�������C��x������ҽ���A1 �� A2 ��
��2����P������C��λ�ڵ�һ��������һ�㣬��A2��A2R��A1P��R����A2R������C����Q����ֱ��PQб�ʵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ȱ�����{![]() }�У�����Ϊq����a1=2��a4=54���Ȳ�����{
}�У�����Ϊq����a1=2��a4=54���Ȳ�����{![]() }�У�����Ϊd��b1=2��b1+b2+b3+b4=a1+ a2+ a3.
}�У�����Ϊd��b1=2��b1+b2+b3+b4=a1+ a2+ a3.
��I��������{![]() }��ͨ�ʽ��
}��ͨ�ʽ��
��II��������{![]() }��ǰn���
}��ǰn���![]() �Ĺ�ʽ��
�Ĺ�ʽ��
��III����![]() ��
��![]() ������n=1��2�������ԱȽ�
������n=1��2�������ԱȽ�![]() ��
��![]() �Ĵ�С����֤����Ľ���.
�Ĵ�С����֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��ǰn���ΪSn �� ������Sn=2��an �� n=1��2��3������
��1��������{an}��ͨ�ʽ��
��2��������{bn}����b1=1����bn+1=bn+an �� ������{bn}��ͨ�ʽ��
��3����cn= ![]() ������{cn}��ǰn���ΪTn=
������{cn}��ǰn���ΪTn= ![]() ����n��
����n��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com