
【题目】如图1是四棱锥的直观图,其正(主)视图和侧(左)视图均为直角三角形,俯视图外框为矩形,相关数据如图2所示.
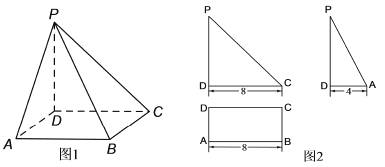
(1)设![]() 中点为
中点为![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求四棱锥
,求四棱锥![]() 的外接球的表面积.
的外接球的表面积.
【答案】(1) 见解析;(2) ![]() .
.
【解析】试题分析:(1)利用中位线定理构造平行四边形,得到![]() ;(2) 由二面角
;(2) 由二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,得到
,得到![]() ,明确外接球的直径即为PB,易得四棱锥
,明确外接球的直径即为PB,易得四棱锥![]() 的外接球的表面积.
的外接球的表面积.
试题解析:
(1)当![]() 是
是![]() 中点时,
中点时, ![]() 平面
平面![]() ,
,
证明如下:取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,
在![]() 中,
中, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() 且
且![]() ,又
,又![]() 是
是![]() 中点,
中点, ![]() ,
,
∴![]() 且
且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
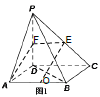
(2)由三视图可得![]() 平面
平面![]() ,
,
在底面![]() 中,过
中,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在底面矩形![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
在![]() 中,又
中,又![]() ,
,
∴![]() ,∴
,∴![]() .
.
由直观图易知四棱锥![]() 的外接球的直径即为
的外接球的直径即为![]() ,
,
∴![]() .
.
故四棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】现有6名奥运会志愿者,其中志愿者![]() 通晓日语,
通晓日语, ![]() 通晓俄语,
通晓俄语, ![]() 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求![]() 被选中的概率;
被选中的概率;
(2)求![]() 和
和![]() 不全被选中的概率;
不全被选中的概率;
(3)若6名奥运会志愿者每小时派两人值班,现有两名只会日语的运动员到来,求恰好遇到![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体;第二次切削沿长方体的对角面刨开,得到两个三棱柱;第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
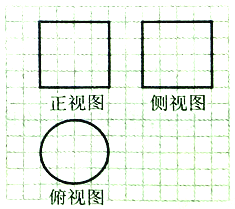
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 为
为![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(-4,0)、B(4,0)
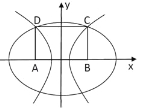
(1)若A、B为椭圆的焦点,且椭圆经过C、D两点,求该椭圆的方程;
(2)若A、B为双曲线的焦点,且双曲线经过C、D两点,求双曲线的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式组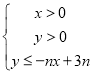 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
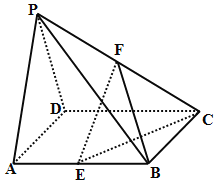
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
(1)求证:EF∥平面PAD;
(2)求三棱锥B-EFC的体积;
(3)求二面角P-EC-D的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com