
已知二次函数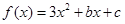 ,不等式
,不等式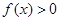 的解集为
的解集为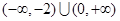 .
.
(1)求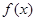 的解析式;
的解析式;
(2)若函数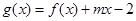 在
在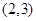 上单调,求实数
上单调,求实数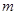 的取值范围;
的取值范围;
(3)若对于任意的x∈[-2,2],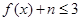 都成立,求实数n的最大值.
都成立,求实数n的最大值.
(1) 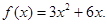 ,(2)
,(2)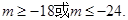 (3)-21.
(3)-21.
解析试题分析:(1) 根据一元二次方程的根与一元二次不等式的解集关系,可列出两个独立条件,求出解析式. 依题得,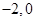 为方程
为方程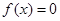 的两个实根,
的两个实根,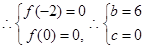
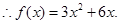
(2)二次函数单调性主要研究对称轴与定义区间相对位置关系,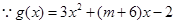 在
在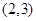 上单调,二次函数开口向上,对称轴
上单调,二次函数开口向上,对称轴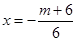
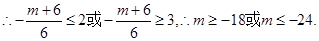 (3)恒成立问题,一般利用变量分离转化为最值问题. 依题得,
(3)恒成立问题,一般利用变量分离转化为最值问题. 依题得,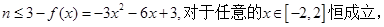 只要
只要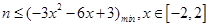 ,设
,设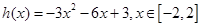
当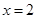 时,
时,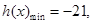
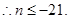 实数n的最大值为
实数n的最大值为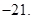
解:(1)依题得,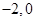 为方程
为方程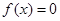 的两个实根, (2分)
的两个实根, (2分)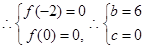 (4分)
(4分)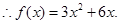 (5分)
(5分)
(2)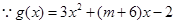 在
在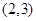 上单调,
上单调,
又二次函数开口向上,对称轴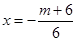 , (7分)
, (7分)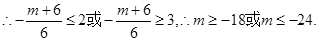 (10分)
(10分)
(3)依题得,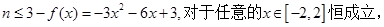 (12分)
(12分)
只要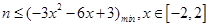 , (13分)
, (13分)
设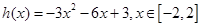
当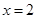 时,
时,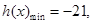 (15分)
(15分)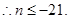 (16分)
(16分)
考点:一元二次方程的根与一元二次不等式的解集关系,二次函数单调性,不等式恒成立


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数 =
=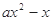 (
( ,
,
(1)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)若函数 与
与 的图像有两个不同的交点
的图像有两个不同的交点 ,求
,求 的取值范围。
的取值范围。
(3)设点 和
和 (
( 是函数
是函数 图像上的两点,平行于
图像上的两点,平行于 的切线以
的切线以 为切点,求证
为切点,求证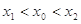 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 ,
, ,
,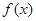 的最小值为
的最小值为 .
.
⑴求函数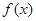 的解析式;
的解析式;
⑵设 ,若
,若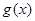 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
⑶设函数 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15—0.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:
(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)的图象与函数h(x)=x+ +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+ ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(1)求水面宽;
(2)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?

(3)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com