
【题目】在平面直角坐标系xOy中,已知P点到两定点D(﹣2,0),E(2,0)连线斜率之积为- ![]() .
.
(1)求证:动点P恒在一个定椭圆C上运动;
(2)过 ![]() 的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
【答案】
(1)证明:设P(x,y),由题意可得kPDkPE=﹣ ![]() ,
,
即有 ![]()
![]() =﹣
=﹣ ![]() ,
,
化为 ![]() =1
=1
(2)解:设过F的直线为x=my+ ![]() ,
,
代入椭圆方程x2+2y2=4,
可得(2+m2)y2+2 ![]() my﹣2=0,
my﹣2=0,
设A(x1,y1),B(x2,y2),
即有y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
x1=my1+ ![]() ,x2=my2+
,x2=my2+ ![]() ,
,
由题意可得,过O的直线x=﹣my交椭圆C于M,N两点,
解得M(﹣ ![]() ,
, ![]() ),N(
),N( ![]() ,﹣
,﹣ ![]() ),
),
可得kAM+kBN= 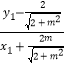 +
+ 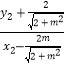 ,
,
通分后的分子=x2y1﹣ ![]() x2﹣
x2﹣ ![]() y1+x1y2+
y1+x1y2+ ![]() x1+
x1+ ![]() y2+
y2+ ![]()
=2my1y2+ ![]() (1+y2)+
(1+y2)+ ![]() (x1﹣x2)+
(x1﹣x2)+ ![]() (y2﹣y1)+
(y2﹣y1)+ ![]()
=﹣ ![]() ﹣
﹣ ![]() +
+ ![]() (y1﹣y2)+
(y1﹣y2)+ ![]() (y2﹣y1)+
(y2﹣y1)+ ![]() =0.
=0.
即有直线AM与直线BN斜率之和为定值0.
【解析】(1)设P(x,y),由题意可得kPDkPE=﹣ ![]() ,运用直线的斜率公式,化简即可得到所求轨迹方程;(2)设过F的直线为x=my+
,运用直线的斜率公式,化简即可得到所求轨迹方程;(2)设过F的直线为x=my+ ![]() ,代入椭圆方程x2+2y2=4,设A(x1 , y1),B(x2 , y2),运用韦达定理,点满足直线方程,再由过O的直线x=﹣my交椭圆C于M,N两点,求得M,N的坐标,运用直线的斜率公式,化简整理,即可得到直线AM与直线BN斜率之和为定值0.
,代入椭圆方程x2+2y2=4,设A(x1 , y1),B(x2 , y2),运用韦达定理,点满足直线方程,再由过O的直线x=﹣my交椭圆C于M,N两点,求得M,N的坐标,运用直线的斜率公式,化简整理,即可得到直线AM与直线BN斜率之和为定值0.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ),若
),若![]() 的一条对称轴离最近的对称中心的距离为
的一条对称轴离最近的对称中心的距离为![]() .
.
(Ⅰ)求![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)在![]() 中角
中角![]() 、
、![]() 、
、![]() 的对边分别是
的对边分别是![]() 满足
满足![]() 恰是
恰是![]() 的最大值,试判断
的最大值,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={m|m∈Z,且|m|≤2018},M的子集S满足:对S中任意3个元素a,b,c(不必不同),都有a+b+c≠0.求集合S的元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市高三上学期期末调研】如图,四面体![]() 中,
中, ![]() 、
、![]() 分别
分别![]() 、
、![]() 的中点,
的中点, ![]() ,
, ![]() .
.
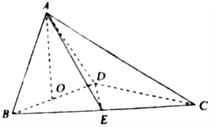
(I)求证: ![]() 平面
平面![]() ;
;
(II)求异面直线![]() 与
与![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设首项为1的正项数列{an}的前n项和为Sn , 且Sn+1﹣3Sn=1.
(1)求证:数列{an}为等比数列;
(2)数列{an}是否存在一项ak , 使得ak恰好可以表示为该数列中连续r(r∈N* , r≥2)项的和?请说明理由;
(3)设 ![]() ,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com