
【题目】已知函数![]() 是自然对数的底数).
是自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,当
,当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)若![]() 且
且![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1) 求出![]() ,
, ![]() 得增区间,
得增区间, ![]() 得减区间;(2)利用导数研究函数
得减区间;(2)利用导数研究函数![]() 的单调性即可求函数
的单调性即可求函数![]() 的最大值;(3)化简已知得
的最大值;(3)化简已知得![]() ,
, ![]()
![]() 即
即![]() ,然后利用分析法证明原不等式.
,然后利用分析法证明原不等式.
试题解析: (1) ![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() ,
, ![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,![]() ,
,![]()
当![]() 时,
时, ![]() ,
,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
![]() .
.
(3) ![]() ,
, ![]()
![]() 即
即![]() .
.
由(1)知 ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,
,
则![]()
要证![]() ,即证
,即证![]() ,即证
,即证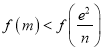 ,即证
,即证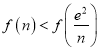 ,
,
即证![]() ,由于
,由于![]() ,即证
,即证![]() .
.
令![]()
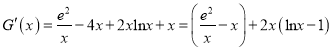
![]()
![]() 恒成立
恒成立
![]() 在
在![]() 递增,
递增, ![]() 在
在![]() 恒成立,
恒成立,
![]() 原不等式成立.
原不等式成立.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的最值、不等式的恒成立,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=kx+b的图象过点(2,1),且b2﹣6b+9≤0
(1)求函数f(x)的解析式;
(2)若a>0,解关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 A﹣BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4. 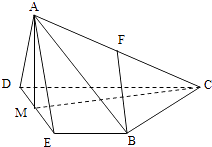
(1)求证:平面 ADE⊥平面BCD;
(2)求证:FB∥平面ADE;
(3)求四棱锥A﹣BCDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刘徽是我国魏晋时期著名的数学家,他编著的《海岛算经》中有一问题:“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高几何?” 意思是:为了测量海岛高度,立了两根表,高均为5步,前后相距1000步,令后表与前表在同一直线上,从前表退行123步,人恰观测到岛峰,从后表退行127步,也恰观测到岛峰,则岛峰的高度为( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0.当直线l被圆C截得的弦长为 ![]() 时,求
时,求
(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C过点P(1,1),且与⊙M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过点P(﹣2,1),
(1)若直线l与直线x+y﹣1=0平行,求直线l的方程;
(2)若点A(﹣1,﹣2)到直线l的距离为1,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() ,直线
,直线![]() 的极坐标方程分别是
的极坐标方程分别是![]() ,
, ![]() .
.
(1)求![]() 与
与![]() 的交点的极坐标;
的交点的极坐标;
(2)设![]() 为
为![]() 的圆心,
的圆心, ![]() 为
为![]() 与
与![]() 的交点连线的中点,已知直线
的交点连线的中点,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),求
为参数),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com