Question

【题目】为了了解初三女生身高情况，某中学对初三女生身高情况进行了一次测量，所得数据整理后列出了频率分布表如下：

组别	频数	频率
145.5～149.5	1	0.02
149.5～153.5	4	0.08
153.5～157.5	20	0.40
157.5～161.5	15	0.30
161.5～165.5	8	0.16
165.5～169.5	m	n
合计	M	N

（1）求出表中m，n，M，N所表示的数分别是多少？
（2）画出频率分布直方图；
（3）全体女生中身高在哪组范围内的人数最多？

Answer 1

【答案】
（1）解：由频率的意义知，N=1，

n=1﹣（0.02+0.08+0.40+0.30+0.16）=0.04，

由第一组的频率和频数，可求得m=2，M=1+4+20+15+8+2=50．

∴m=2，n=0.04，M=50，N=1．

（2）解：频率分布直方图如图．

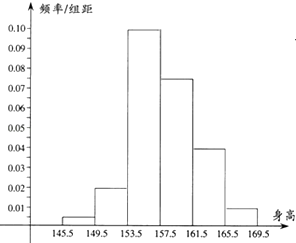
（3）解：由频率分步表可得全体女生中身高在153.5～157.5这一组范围内的人数最多，为20人．
【解析】（1）由频率的意义知，N=1，n=1﹣（0.02+0.08+0.40+0.30+0.16），由第一组的频率和频数，可求得m=2，M=1+4+20+15+8+2，从而得到结论．（2）频率分布直方图如图．（3）由频率分步表可得全体女生中身高在153.5～157.5这一组范围内的人数最多．
【考点精析】本题主要考查了频率分布直方图和用样本的频率分布估计总体分布的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；样本数据的频率分布表和频率分布直方图，是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律，它可以让我们更清楚的看到整个样本数据的频率分布情况，并由此估计总体的分布情况才能正确解答此题．