Question

【题目】如图，四棱锥中，平面平面,// ,,

,且，.

（1）求证：平面；

（2）求和平面所成角的正弦值；

（3）在线段上是否存在一点使得平面平面，请说明理由.

Answer 1

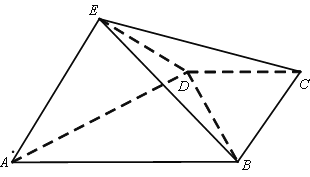
【答案】（1）证明过程详见解析；（2）；（3）在线段上存在一点使得平面平面.

【解析】

试题分析：本题主要考查线线垂直、线面垂直、面面垂直、线面角、向量法等基础知识，考查学生的空间想象能力、逻辑推理能力、计算能力、转化能力.第一问，在中，求出，在中，求出， 在中，三边符合勾股定理，所以， 利用面面垂直的性质，得平面； 第二问，利用第一问的证明得到垂直关系，建立空间直角坐标系，得到平面BDF和平面CDE中各点的坐标，得出向量坐标，先求出平面CDE的法向量，利用夹角公式求BE和平面CDE所成的角的正弦值；第三问，假设存在F，使得，用表示，求出平面BEF的法向量，由于两个平面垂直，则两个法向量垂直，则， 解出.

（1）由，.,

可得．

由，且，

可得．

又．

所以．

又平面平面，

平面 平面 ，

平面，

所以平面．　　　　　　　　　 ５分

（2）如图建立空间直角坐标系，

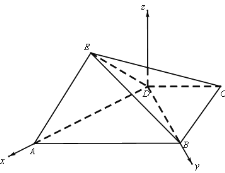
则，，，，

，，．

设是平面的一个法向量，则，，

即

令，则．

设直线与平面所成的角为，

则．

所以和平面所成的角的正弦值．　　　　　　 1０分

（3）设，．

，，.

则．

设是平面一个法向量，则，，

即

令，则．

若平面平面，则，即，.

所以，在线上存在一点使得平面平面. 14分