
(本小题11分) 在7块大小及条件相同的试验田上施肥,做肥量对小麦产量影响的试验,得到如下一组数据:
|
施化肥量x |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
小麦产量 |
330 |
345 |
365 |
405 |
445 |
450 |
455 |
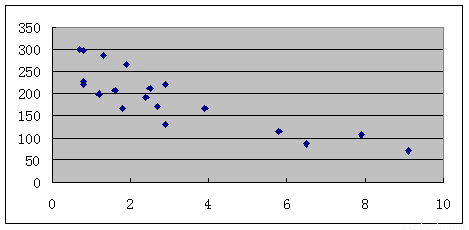
(1)画出散点图;
(2)对x与y进行线性回归分析,并预测施肥量30时小麦的产量为多少?
(1)见解析;(2)回归直线方程为: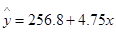
当x=50时,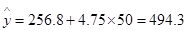 也自是说当施化肥量为50时,小麦的产量大致接近494.3. 回归系数
也自是说当施化肥量为50时,小麦的产量大致接近494.3. 回归系数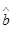 =4.75反映出当化肥施加量增加1个单位,小麦的产量将增加4.75,而256.8是不受施化肥量影响的部分。
=4.75反映出当化肥施加量增加1个单位,小麦的产量将增加4.75,而256.8是不受施化肥量影响的部分。
【解析】
试题分析:(1) 画出散点图如图:
(2)根据已知数据表得拓展表如下:
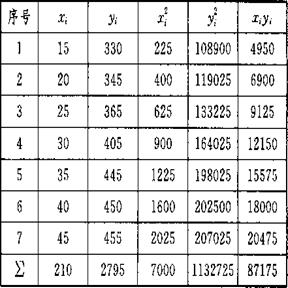
由表易得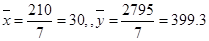
代人线性相关系数公式得
因此y与x有紧密的线性相关关系, 回归系数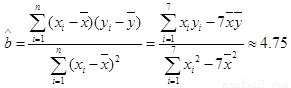
所以回归直线方程为: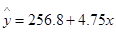
当x=50时,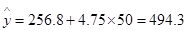 也自是说当施化肥量为50时,小麦的产量大致接近494.3. 回归系数
也自是说当施化肥量为50时,小麦的产量大致接近494.3. 回归系数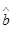 =4.75反映出当化肥施加量增加1个单位,小麦的产量将增加4.75,而256.8是不受施化肥量影响的部分
=4.75反映出当化肥施加量增加1个单位,小麦的产量将增加4.75,而256.8是不受施化肥量影响的部分
考点:本题主要考查回归分析的概念及思想方法。
点评:典型题,散点图给出定性结论,利用所给数据确定线性回归方程,作出较准确判断。


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源:2012-2013学年浙江省高二上期中考试理科数学试卷(解析版) 题型:解答题
(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。
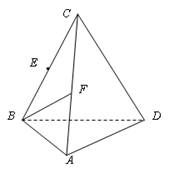
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在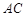 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高二上期中考试理科数学试卷(解析版) 题型:解答题
(本小题11分)如图,在四棱锥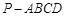 中,
中,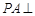 平面
平面 ,
,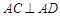 ,
,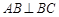 ,
, ,
,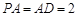 ,
,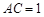 .
.
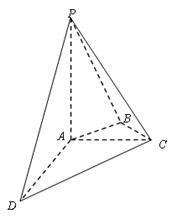
(1)证明: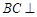 平面
平面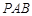
(2)求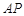 和平面
和平面 所成角的正弦值
所成角的正弦值
(3)求二面角 的正切值;
的正切值;
查看答案和解析>>
科目:高中数学 来源:福建省2009-2010下学期学段考试卷高一数学试题 题型:解答题
本小题11分
已知圆 的圆心坐标为
的圆心坐标为 ,若圆
,若圆 与
与 轴相切,在直线
轴相切,在直线 上截得的弦长为
上截得的弦长为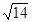 ,且圆心在直线
,且圆心在直线 上。
上。
(1)求圆 的方程。
的方程。
(2)若点 圆
圆 上,求
上,求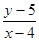 的取值范围。
的取值范围。
(3)将圆 向左平移一个单位得圆
向左平移一个单位得圆 ,若直线
,若直线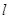 与两坐标轴正半轴的交点分别为
与两坐标轴正半轴的交点分别为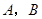 ,直线
,直线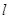 的方程为
的方程为 。当
。当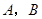 在坐标轴上滑动且
在坐标轴上滑动且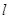 与圆
与圆 相切时,求
相切时,求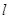 与两坐标轴正半轴围成面积的最小值
与两坐标轴正半轴围成面积的最小值
查看答案和解析>>
科目:高中数学 来源:福建省2009-2010下学期学段考试卷高一数学试题 题型:解答题
本小题11分
已知数列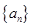 是等差数列,
是等差数列,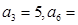 11且,
11且,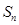 是数列
是数列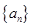 的前
的前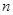 项和。
项和。
(1)求数列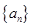 的通项公式
的通项公式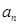 及前
及前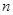 项和
项和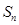 。
K^S*5U.C
。
K^S*5U.C
(2)设正项等比数列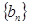 满足
满足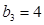 ,
,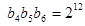 ,数列
,数列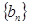 的通项公式
的通项公式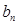
(3)在(2)的条件下若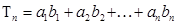 ,求
,求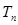 的值。 K^S*5U.C
的值。 K^S*5U.C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com