【答案】
分析:(1)由f′(x)=3ax
2+2bx+c和f(x)在(x
,f(x
))处的切线斜率k=(x
-2)(x
+1),能求出求a,b,c的值.
(2)由f′(x)=x
2-x-2=(x-2)(x+1),能求出函数f(x)的单调区间.
(3)由f′(x)=(x-2)(x+1)及-3≤x≤2,列表能求出函数f(x)在R上的极大值.
解答:解:(1)f′(x)=3ax
2+2bx+c,(1分)
而f(x)在(x
,f(x
))处的切线斜率k=f′(x
)=3ax
2+2bx
+c=(x
-2)(x
+1),
∴3a=1,2b=-1,c=-2,
∴a=

,b=-

,c=-2.(3分)
(2)∵f(x)=
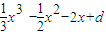
,
由f′(x)=x
2-x-2
=(x-2)(x+1)≥0,
知f(x)在(-∞,-1]和[2,+∞)上是增函数,
由f′(x)=(x-2)(x+1)≤0,
知f(x)在[-1,2]上为减函数.(7分)
(3)由f′(x)=(x-2)(x+1)及-3≤x≤2,可列表
| x | [-3,-1) | -1 | (-1,2] |
| f′(x) | + | | - |
| f(x) | ↑ | 极大值 | ↓ |
f(x)在[-3,2]上的最小值产生于f(-3)和f(2),
由f(-3)=-
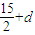
,f(2)=
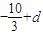
,
知f(-3)<f(2),(9分)
于是f(-3)=-
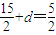
,
则d=10.(11分)
∴f(x)
max=f(-1)=
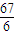
,
即所求函数f(x)在R上的极大值为
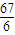
.(12分)
点评:本题考查函数的切线方程、单调区间和极值,综合性强,难度大,计算繁琐,容易出错.解题时要认真审题,仔细解答,注意导数的性质的灵活运用.

 ,求y=f(x)在R上的极大值.
,求y=f(x)在R上的极大值. ,b=-
,b=- ,c=-2.(3分)
,c=-2.(3分)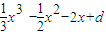 ,
,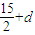 ,f(2)=
,f(2)=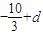 ,
,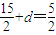 ,
,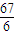 ,
,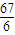 .(12分)
.(12分)
