
对于数列 ,若满足
,若满足 ,则称数列
,则称数列 为“0-1数列”.定义变换
为“0-1数列”.定义变换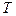 ,
,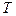 将“0-1数列”
将“0-1数列” 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如 :1,0,1,则
:1,0,1,则 设
设 是“0-1数列”,令
是“0-1数列”,令
 .
.
(Ⅰ) 若数列 :
: 求数列
求数列 ;
;
(Ⅱ) 若数列 共有10项,则数列
共有10项,则数列 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若 为0,1,记数列
为0,1,记数列 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为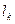 ,
, .求
.求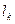 关于
关于 的表达式.
的表达式.
解:(Ⅰ)由变换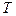 的定义可得
的定义可得 …………………………2分
…………………………2分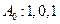 ………………………………4分
………………………………4分
(Ⅱ) 数列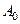 中连续两项相等的数对至少有10对 ………………………………5分
中连续两项相等的数对至少有10对 ………………………………5分
证明:对于任意一个“0-1数列” ,
, 中每一个1在
中每一个1在 中对应连续四项1,0,0,1,在
中对应连续四项1,0,0,1,在 中每一个0在
中每一个0在 中对应的连续四项为0,1,1,0,
中对应的连续四项为0,1,1,0,
因此,共有10项的“0-1数列” 中的每一个项在
中的每一个项在 中都会对应一个连续相等的数对,
中都会对应一个连续相等的数对,
所以 中至少有10对连续相等的数对. ……………………………8分
中至少有10对连续相等的数对. ……………………………8分
(Ⅲ) 设 中有
中有 个01数对,
个01数对, 中的00数对只能由
中的00数对只能由 中的01数对得到,所以
中的01数对得到,所以 ,
, 中的01数对有两个产生途径:①由
中的01数对有两个产生途径:①由 中的1得到; ②由
中的1得到; ②由 中00得到,
中00得到,
由变换 的定义及
的定义及 可得
可得 中0和1的个数总相等,且共有
中0和1的个数总相等,且共有 个,
个,
所以 ,
,
所以 ,
,
由 可得
可得 ,
,
所以 ,
,
当 时,
时,
若 为偶数,
为偶数,



上述各式相加可得 ,
,
经检验, 时,也满足
时,也满足
若 为奇数,
为奇数,



上述各式相加可得 ,
,
经检验, 时,也满足
时,也满足
所以 …………………………………………..13分
…………………………………………..13分
解析


科目:高中数学 来源:2010-2011学年北京市海淀区高三第二学期第二次模拟(理科)数学题 题型:解答题
对于数列 ,若满足
,若满足 ,则称数列
,则称数列 为“0-1数列”.定义变换
为“0-1数列”.定义变换 ,
, 将“0-1数列”
将“0-1数列” 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如 :1,0,1,则
:1,0,1,则 设
设 是“0-1数列”,令
是“0-1数列”,令
 .
.
(Ⅰ)
若数列 :
: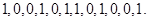 求数列
求数列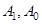 ;
;
(Ⅱ)
若数列 共有10项,则数列
共有10项,则数列 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若 为0,1,记数列
为0,1,记数列 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为 ,
, .求
.求 关于
关于 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共13分)
对于数列![]() ,若满足
,若满足![]() ,则称数列
,则称数列![]() 为“0-1数列”.定义变换
为“0-1数列”.定义变换![]() ,
,![]() 将“0-1数列”
将“0-1数列”![]() 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如![]() :1,0,1,则
:1,0,1,则![]() 设
设![]() 是“0-1数列”,令
是“0-1数列”,令![]()
![]() .
.
(Ⅰ) 若数列![]() :
:![]() 求数列
求数列![]() ;
;
(Ⅱ) 若数列![]() 共有10项,则数列
共有10项,则数列![]() 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若![]() 为0,1,记数列
为0,1,记数列![]() 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为![]() ,
,![]() .求
.求![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于数列![]() ,若满足
,若满足![]() ,则称数列
,则称数列![]() 为“0-1数列”.定义变换
为“0-1数列”.定义变换![]() ,
,![]() 将“0-1数列”
将“0-1数列”![]() 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如![]() :1,0,1,则
:1,0,1,则![]() 设
设![]() 是“0-1数列”,令
是“0-1数列”,令![]()
![]() 3,….
3,….
(Ⅰ) 若数列![]() :
:![]() 求数列
求数列![]() ;
;
(Ⅱ) 若数列![]() 共有10项,则数列
共有10项,则数列![]() 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若![]() 为0,1,记数列
为0,1,记数列![]() 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为![]() ,
,![]() .求
.求![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于数列![]() ,若满足
,若满足![]() ,则称数列
,则称数列![]() 为“0-1数列”.定义变换
为“0-1数列”.定义变换![]() ,
,![]() 将“0-1数列”
将“0-1数列”![]() 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如
中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如![]() :1,0,1,则
:1,0,1,则![]() 设
设![]() 是“0-1数列”,令
是“0-1数列”,令![]()
![]() .
.
(Ⅰ) 若数列![]() :
:![]() 求数列
求数列![]() ;
;
(Ⅱ) 若数列![]() 共有10项,则数列
共有10项,则数列![]() 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若![]() 为0,1,记数列
为0,1,记数列![]() 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为![]() ,
,![]() .求
.求![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com