
[2012·陕西卷] 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=![]() .
.
(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=![]() ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
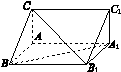
图1-7
科目:高中数学 来源: 题型:
[2012·陕西卷] 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=![]() .
.
(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=![]() ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
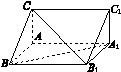
图1-7
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012·陕西卷)两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )
A.10种 B.15种
C.20种 D.30种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com