
����Ŀ��ij��У����15000�ˣ���������10500�ˣ�Ů��4500�ˣ�Ϊ�����Уѧ��ÿ��ƽ�������˶�ʱ�����������÷ֲ�����ķ������ռ�300λѧ��ÿ��ƽ�������˶�ʱ����������ݣ���λ:Сʱ��
��1��Ӧ�ռ�����λŮ���������ݣ�
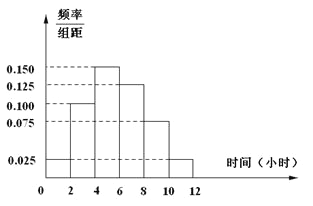
��2��������300���������ݣ��õ�ѧ��ÿ��ƽ�������˶�ʱ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ�������Ϊ��![]() .���Ƹ�Уѧ��ÿ��ƽ�������˶�ʱ�䳬��4��Сʱ�ĸ���.
.���Ƹ�Уѧ��ÿ��ƽ�������˶�ʱ�䳬��4��Сʱ�ĸ���.
��3�������������У���60λŮ����ÿ��ƽ�������˶�ʱ�䳬��4��Сʱ.�����ÿ��ƽ�������˶�ʱ�����Ա�������������ж��Ƿ���![]() �İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
�İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
����
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
���𰸡���1��90����2��0.75����3����![]() �İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
�İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
��������
�����������1�����÷ֲ������Ӧ�ÿ������![]() ����Ӧ�ռ�90λŮ������������.��2������Ƶ�ʷֲ�ֱ��ͼ�ɵ�
����Ӧ�ռ�90λŮ������������.��2������Ƶ�ʷֲ�ֱ��ͼ�ɵ�![]() .��3����������300λѧ������
.��3����������300λѧ������![]() �˵�ÿ��ƽ�������˶�ʱ�䳬��4Сʱ��75�˵�ÿ��ƽ�������˶�ʱ�䲻����4Сʱ.����Ϊ������������210���ǹ��������ģ�90���ǹ���Ů����.���Ի���ÿ��ƽ�������˶�ʱ�����Ա�������������
�˵�ÿ��ƽ�������˶�ʱ�䳬��4Сʱ��75�˵�ÿ��ƽ�������˶�ʱ�䲻����4Сʱ.����Ϊ������������210���ǹ��������ģ�90���ǹ���Ů����.���Ի���ÿ��ƽ�������˶�ʱ�����Ա�������������![]() .����
.����![]() �İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
�İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
��1��![]() ������Ӧ�ռ�90λŮ������������.
������Ӧ�ռ�90λŮ������������.
��Ƶ�ʷֲ�ֱ��ͼ��![]() ����Уѧ��ÿ��ƽ�������˶�ʱ�䳬��4��Сʱ�ĸ���Ϊ
����Уѧ��ÿ��ƽ�������˶�ʱ�䳬��4��Сʱ�ĸ���Ϊ![]() .
.
�ɣ�2��֪��300λѧ������![]() �˵�ÿ��ƽ�������˶�ʱ�䳬��4Сʱ��75�˵�ÿ��ƽ�������˶�ʱ�䲻����4Сʱ.����Ϊ������������210���ǹ��������ģ�90���ǹ���Ů����.����ÿ��ƽ�������˶�ʱ�����Ա����������£�
�˵�ÿ��ƽ�������˶�ʱ�䳬��4Сʱ��75�˵�ÿ��ƽ�������˶�ʱ�䲻����4Сʱ.����Ϊ������������210���ǹ��������ģ�90���ǹ���Ů����.����ÿ��ƽ�������˶�ʱ�����Ա����������£�
ÿ��ƽ�������˶�ʱ�����Ա�������
���� | Ů�� | �ܼ� | |
ÿ��ƽ�������˶�ʱ�䲻����4Сʱ | 45 | 30 | 75 |
ÿ��ƽ�������˶�ʱ�䳬��4Сʱ | 165 | 60 | 225 |
�ܼ� | 210 | 90 | 300 |
��������������![]() .
.
��![]() �İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.
�İ�����Ϊ����Уѧ����ÿ��ƽ�������˶�ʱ�����Ա��й���.


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
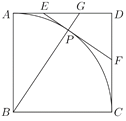
����Ŀ����ͼ���ڱ߳�Ϊ6��������![]() �У���
�У���![]() ��Բ��Ϊ
��Բ��Ϊ![]() ������
������![]() �ϵĵ�
�ϵĵ�![]() ����
����![]() �����ߣ���
�����ߣ���![]() ��
��![]() �ֱ��ཻ�ڵ�
�ֱ��ཻ�ڵ�![]() ��
��![]() ��
��![]() ���ӳ��߽�
���ӳ��߽�![]() ���ڵ�
���ڵ�![]() .
.
��1����![]() ��
��![]() ����
����![]() ��
��![]() ֮��ĺ�������ʽ����д������������
֮��ĺ�������ʽ����д������������
��2����![]() ʱ����
ʱ����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������С������һ�˶�����������ȫ�����������Ӱ�����ĵ��������˶�֮һ���������������˶�����֮һ���DZ�������֯��������֯ս����Ϻͽ������ŵ���Ҫ�ֶΣ��������Ҳ�������˶�������һ�֣��ǽ��Է����ƻ�����ռΪ���У����ƻ��Է�����Ŀ��Ƶļ������DZ���������ת������Ҫ�ֶΣ��������˶���������Ҫ���˶�Ա����ȷ�жϺ�ѡ�����мס������ӽ���������������A��B�����˶�Ա�ǼӶ�Ա��C���ҶӶ�Ա��B��A����������A��B���20m��C��A����������A��C���14![]() m����A�ر�ƫ��60�㷽��ˮƽ��������Ϊ10
m����A�ر�ƫ��60�㷽��ˮƽ��������Ϊ10![]() m/s��ͬʱB�ر�ƫ��30�㷽����10m/s���ٶ�ǰ������CͬʱҲ��10m/s���ٶ�ǰȥ����������B��C����ͬһƽ���˶����Ҿ���������ֱ���˶���
m/s��ͬʱB�ر�ƫ��30�㷽����10m/s���ٶ�ǰ������CͬʱҲ��10m/s���ٶ�ǰȥ����������B��C����ͬһƽ���˶����Ҿ���������ֱ���˶���
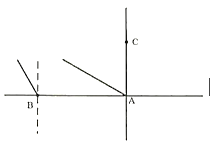
��1����C����ƫ��60�㷽��ǰȥ�������ж�B�ܷ�ӵ�����˵�����ɣ�
��2����C�ı䣨1���ķ���ǰȥ�������ж�C�ܷ���ɹ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x����2cos2x��cos��2x��![]() ����
����
��1����f��x�������ں����ֵ��
��2����֪��ABC�У���A.B.C�ĶԱ߷ֱ�ΪA��B��C����f������A����![]() ��b+c��2����a����Сֵ��
��b+c��2����a����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס�������ѧ����ѡ��һ�˲μ����������Ϊ����Ҫ�����ǵ����ˮƽ���в��ԣ���������ѧ������ͬ�����¸����10�Σ����еĻ������£�
�� | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
�� | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)����ס�������������л�����ƽ�����ͱ��
(2)�Ƚ������˵ijɼ���Ȼ�����ѡ������ѧ���μ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={-4��2a-1��a2}��B={a-5��1-a��9}���ֱ����ʺ�����������a��ֵ��
(1)9��(A��B)��(2){9}=A��B��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�еļ��������������й�ͬ�����Բ��ɣ���֪����Բ�Ķ���ֱ�ΪP��Q���߷ֱ�Ϊ2��1������뾶Ϊ1��AΪ����Բ���ϵĶ��㣬BΪ����Բ���ϵĶ��㣨����A�غϣ��������ĸ����ۣ�
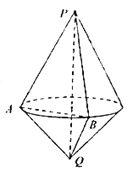
������![]() ��������ֵΪ
��������ֵΪ![]() ��
��
��ֱ��PB��ƽ��PAQ���ɽǵ����ֵΪ![]() ��
��
����ֱ��BQ��AP���ɽ���Сʱ��������ֵΪ![]() ��
��
��ֱ��BQ��AP���ɽǵ����ֵΪ![]() ��
��
������ȷ�Ľ�����___________.��д��������ȷ���۵ı�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������Ϊ![]() �ϵĺ���
�ϵĺ���![]() ����һ�����������ߵ�һ�������.���ø�ͼ�ṩ����Ϣ������漸������.
����һ�����������ߵ�һ�������.���ø�ͼ�ṩ����Ϣ������漸������.

��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ���ڵķ���
���ڵķ���![]() ��������ͬ�⣬��
��������ͬ�⣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У�������Ϊ�� ��
A.�����ı���ȵ��ı��β���������
B.z1 �� z2��C��z1+z2Ϊʵ���ij�ֱ�Ҫ������z1 �� z2��Ϊ�����
C.��x��y��R����x+y��2����x��y������һ������1
D.��������n��N* �� ![]() +
+ ![]() +��+
+��+ ![]() ����ż��
����ż��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com