Question

【题目】某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元．某月甲、乙两户共交水费y元，已知甲、乙两用户该月用水量分别为5x，3x吨． （Ⅰ） 若x=1，求该月甲、乙两户的水费；
（Ⅱ） 求y关于x的函数；
（Ⅲ） 若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量．

Answer 1

【答案】解：（Ⅰ）由题意可得，当x=1，求该月甲户的水费为5吨，该月乙户的水费为3吨．

（Ⅱ）当5x≤4时，即x≤ 时，y=（5x+3x）×1.8=14.4x；

当3x≤4＜5x 时，即 ＜x≤ 时，y=3x×1.8+4×1.8+（5x﹣4）×3=20.4x﹣4.8；

当3x＞4，即x＞ 时，y=（4+4）×1.8+（3x﹣4+5x﹣4）×3=24x﹣9.6，

综上可得，y关于x的函数为y= ．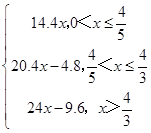

（Ⅲ） 若甲、乙两户该月共交水费26.4元，∵14.4x≤14.4× ＜26.4，故x不满足x≤ ；

∵20.4× ﹣4.8＜26.4＜ ×20.4﹣4.8，∴x∈（ ， ]，故有20.4x﹣4.8=26.4，求得x≈1.53，

故甲户的水费为5×1.53=7.65吨，该月乙户的水费为3×1.53=4.59吨

【解析】（Ⅰ） 若x=1，求该月甲、乙两户的水费分别为5x、3x吨的值．（Ⅱ） 分三种情况，分别求得y的解析式，综合可得结论．（Ⅲ） 先判断x的范围，确定函数得解析式，求出x的值，可得甲、乙两户的水费分别为5x、3x吨的值．