
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
(本题可以参考两个分类变量x和y有关系的可信度表:)
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
由图看出显然一个交点,因此函数![]() 的零点个数只有一个
的零点个数只有一个
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
查看答案和解析>>
科目:高中数学 来源:2014届广东省东莞市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
|
|
患色盲 |
不患色盲 |
总计 |
|
男 |
|
442 |
|
|
女 |
6 |
|
|
|
总计 |
44 |
956 |
1000 |
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?
随机变量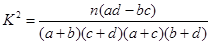
附临界值参考表:
|
P(K2≥x0) |
0.10 |
0.05 |
0.025 |
0.10 |
0.005 |
0.001 |
|
x0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
查看答案和解析>>
科目:高中数学 来源:2013届内蒙古赤峰市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(Ⅰ)根据以上的数据建立一个2×2的列联表;
(Ⅱ)若认为“性别与患色盲有关系”,则出错的概率会是多少.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学变量间的相关关系、统计案例专项训练(河北) 题型:解答题
在研究色盲与性别的关系调查中,调查了男性480人,其中有38有患色盲,调查的520个女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?附临界值参考表:
|
P(K2≥x0) |
0.10 |
0.05 |
0.025 |
0.10 |
0.005 |
0.001 |
|
x0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com