
 ,
, 
 ,使
,使 在
在 上的最小值为
上的最小值为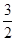 ,若存在,求出
,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。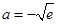 ,使
,使 在
在 上的最小值为
上的最小值为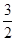
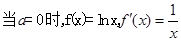 . 1分
. 1分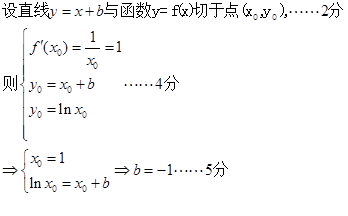
 ,使
,使 在
在 上的最小值为
上的最小值为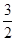 ,
,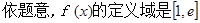 .
.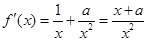 ………6分
………6分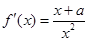 =0,得
=0,得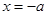 ………7分
………7分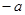 与区间
与区间 的相对位置讨论,
的相对位置讨论,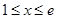
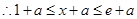
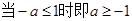 ,则
,则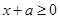 ,
,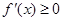 在
在 上恒成立,此时
上恒成立,此时 在
在 上为增函数, 8分
上为增函数, 8分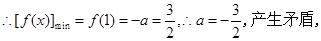 (舍去). 9分
(舍去). 9分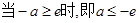 ,则
,则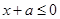 ,即
,即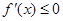 在
在 上恒成立,
上恒成立, 在
在 上为减函数, 10分
上为减函数, 10分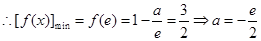 (舍去).………11分
(舍去).………11分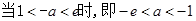 , (方法1):列表如下
, (方法1):列表如下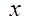 | 1 | 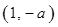 | 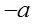 | 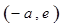 | 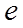 |
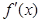 | | 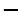 | 0 | 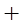 | |
 | 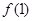 | ↙ | 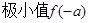 | ↗ | 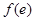 |
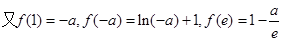 ………12分
………12分
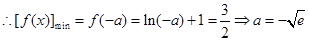 ………13分
………13分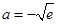 ,使
,使 在
在 上的最小值为
上的最小值为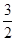 ………14分
………14分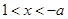 时,
时,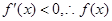 在
在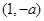 上为减函数,
上为减函数,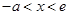 时,
时,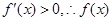 在
在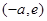 上为增函数,………12分
上为增函数,………12分
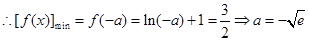 , ………13分
, ………13分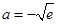 ,使
,使 在
在 上的最小值为
上的最小值为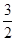 ………14分
………14分

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com