
【题目】有下列几个命题:①“若p,则q”的否命题是“若![]() ,则
,则![]() ”;②p是q的必要条件,r是q的充分不必要条件,则p是r的必要不充分条件;③若“
”;②p是q的必要条件,r是q的充分不必要条件,则p是r的必要不充分条件;③若“![]() ”为真命题,则命题p,q中至多有一个为真命题;④过点
”为真命题,则命题p,q中至多有一个为真命题;④过点![]() 的直线和圆
的直线和圆![]() 相切的充要条件是直线斜率为
相切的充要条件是直线斜率为![]() .其中为真命题的有( )
.其中为真命题的有( )
A.①②B.①②③C.①③④D.①②③④
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线![]() ,一光源在点
,一光源在点![]() 处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点
处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点![]() ,反射后,又射向抛物线上的点
,反射后,又射向抛物线上的点![]() ,再反射后又沿平行于抛物线的对称轴方向射出,途中遇到直线
,再反射后又沿平行于抛物线的对称轴方向射出,途中遇到直线![]() 上的
上的![]() 点,再反射后又射回点
点,再反射后又射回点![]() .设
.设![]() ,
,![]() 两点的坐标分别是
两点的坐标分别是![]() ,
,![]() .
.
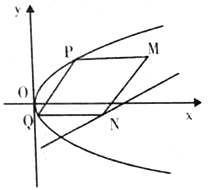
(1)证明:![]() ;
;
(2)若四边形![]() 是平行四边形,且点
是平行四边形,且点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着网络的普及,数码产品早已走进千家万户的生活,为了节约资源,促进资源循环利用,折旧产品回收行业得到迅猛发展,电脑使用时间越长,回收价值越低,某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计,得到如图所示的频率分布直方图,在如图对时间使用的分组中,将使用时间落入各组的频率视为概率.
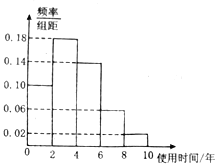
(1)若在该市场随机选取1个2018年成交的二手电脑,求其使用时间在![]() 上的概率;
上的概率;
(2)根据电脑交易市场往年的数据,得到如图所示的散点图及一些统计量的值,其中![]() (单位:年)表示折旧电脑的使用时间,
(单位:年)表示折旧电脑的使用时间,![]() (单位:百元)表示相应的折旧电脑的平均交易价格.
(单位:百元)表示相应的折旧电脑的平均交易价格.

由散点图判断,可采用![]() 作为该交易市场折旧电脑平均交易价格与使用年限
作为该交易市场折旧电脑平均交易价格与使用年限![]() 的回归方程,若
的回归方程,若![]() ,
,![]() ,选用如下参考数据,求
,选用如下参考数据,求![]() 关于
关于![]() 的回归方程,并预测在区间
的回归方程,并预测在区间![]() (用时间组的区间中点值代表该组的值)上折旧电脑的价格.
(用时间组的区间中点值代表该组的值)上折旧电脑的价格.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
附:参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: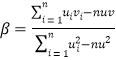 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的较大数)为
表示a、b中的较大数)为![]() 、
、![]() 两点的“切比雪夫距离”.
两点的“切比雪夫距离”.
(1)若![]() ,Q为直线
,Q为直线![]() 上动点,求P、Q两点“切比雪夫距离”的最小值;
上动点,求P、Q两点“切比雪夫距离”的最小值;
(2)定点![]() ,动点
,动点![]() 满足
满足![]()
![]() ,请求出P点所在的曲线所围成图形的面积.
,请求出P点所在的曲线所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com